2007 II: Unterschied zwischen den Versionen
| Zeile 81: | Zeile 81: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
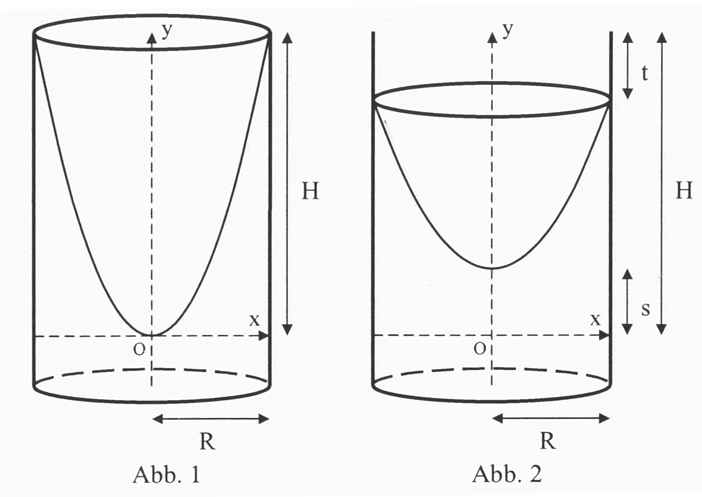
Ein kreiszylindrischer Becher, der zum Teil mit Wasser gefüllt ist, rotiert mit konstanter Rotationsgeschwindigkeit um seine Symmetrieachse. Die Oberfläche der Flüssigkeit ist eine Drehfläche, die durch Rotation einer Parabel entsteht. Die Symmetrieachse der Parabel fällt dabei mit der Symmetrieachse des Bechers zusammen. | Ein kreiszylindrischer Becher, der zum Teil mit Wasser gefüllt ist, rotiert mit konstanter Rotationsgeschwindigkeit um seine Symmetrieachse. Die Oberfläche der Flüssigkeit ist eine Drehfläche, die durch Rotation einer Parabel entsteht. Die Symmetrieachse der Parabel fällt dabei mit der Symmetrieachse des Bechers zusammen. | ||
| − | + | [[Bild:Zeichnung,Infini-II-07.jpg]] | |
Das Koordinatensystem ist so gewählt, dass die zu Abb. 1 gehörende | Das Koordinatensystem ist so gewählt, dass die zu Abb. 1 gehörende | ||
Parabel die Gleichung <math>y =\frac{H}{R^2}x^2</math> | Parabel die Gleichung <math>y =\frac{H}{R^2}x^2</math> | ||
Version vom 19. Februar 2010, 10:01 Uhr
|
|
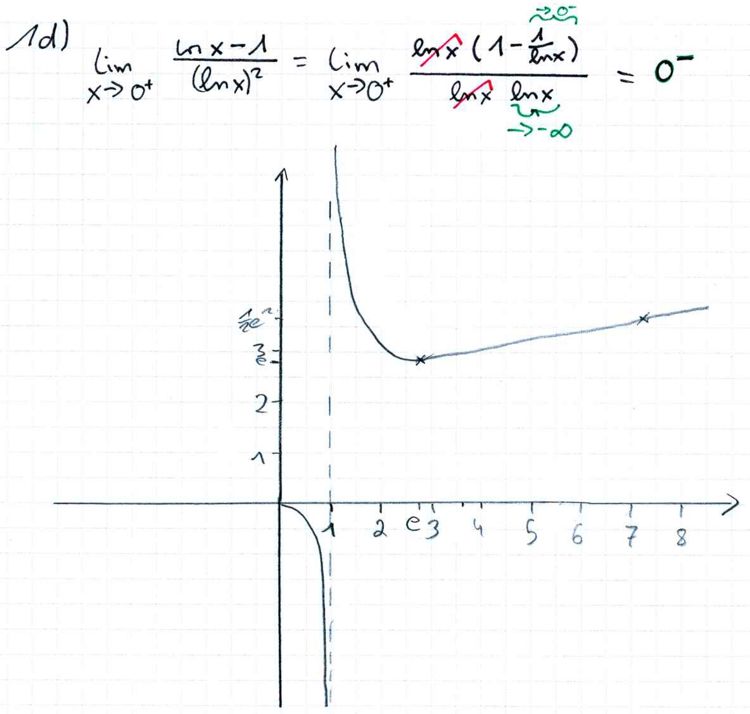
1. Gegeben ist die Funktion
|
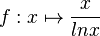 mit dem maximalen Definitionsbereich Df = IR+ \ {1}. Der Graph von f wird mit Gf bezeichnet.
mit dem maximalen Definitionsbereich Df = IR+ \ {1}. Der Graph von f wird mit Gf bezeichnet.
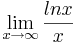 = 0 darf ohne Beweis verwendet werden.)
= 0 darf ohne Beweis verwendet werden.)

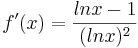 ]
]


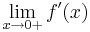 und skizzieren Sie Gf unter Verwendung der bisherigen Ergebnisse in ein Koordinatensystem.
und skizzieren Sie Gf unter Verwendung der bisherigen Ergebnisse in ein Koordinatensystem.
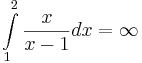 .
Was folgt für
.
Was folgt für  ? Begründen Sie Ihre Antwort. Dabei dürfen Sie
ohne Nachweis verwenden, dass für x >1 gilt: ln x < x −1.
? Begründen Sie Ihre Antwort. Dabei dürfen Sie
ohne Nachweis verwenden, dass für x >1 gilt: ln x < x −1.
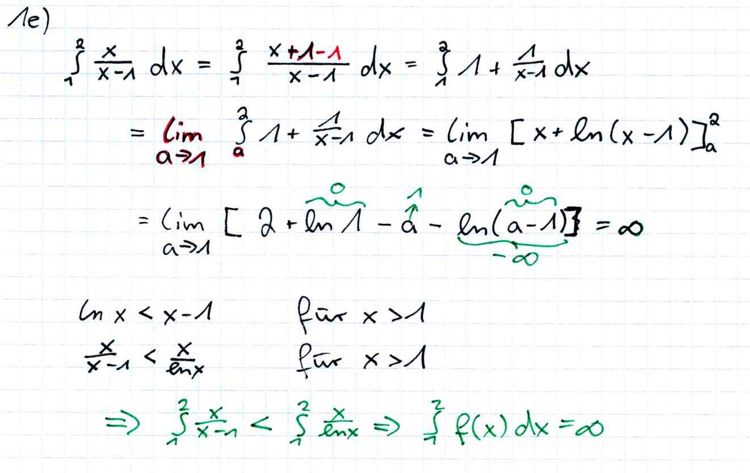
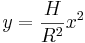 besitzt.
besitzt.



