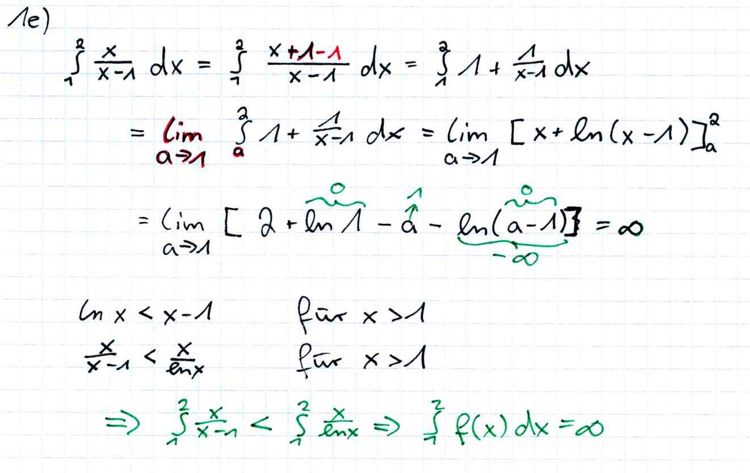2007 II: Unterschied zwischen den Versionen
| Zeile 10: | Zeile 10: | ||
| − | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=2ad4ccef77e003c1a9ba1d85ca3ba82a '''Download der Originalaufgaben: Abitur 2007 LK Mathematik Bayern''' | + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=2ad4ccef77e003c1a9ba1d85ca3ba82a '''Download der Originalaufgaben: Abitur 2007 LK Mathematik Bayern''']</center> |
| Zeile 66: | Zeile 66: | ||
[[Bild:Infini07-1e.jpg|750px]] | [[Bild:Infini07-1e.jpg|750px]] | ||
}} | }} | ||
| + | |||
| + | |||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 2 | ||
Version vom 19. Februar 2010, 08:51 Uhr
|
|
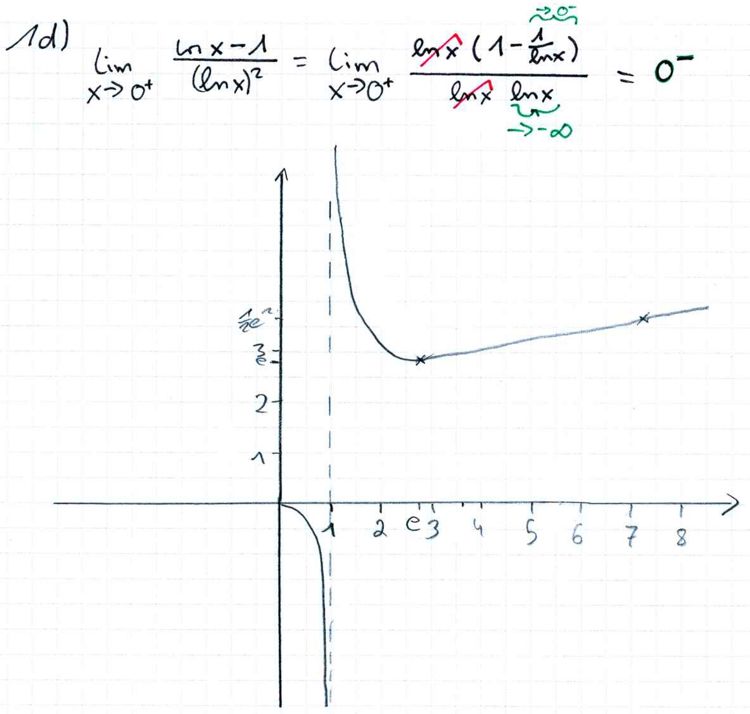
1. Gegeben ist die Funktion
|
|
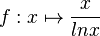 mit dem maximalen Definitionsbereich Df = IR+ \ {1}. Der Graph von f wird mit Gf bezeichnet.
mit dem maximalen Definitionsbereich Df = IR+ \ {1}. Der Graph von f wird mit Gf bezeichnet.

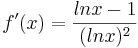 ]
]