2007 II: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
| Zeile 39: | Zeile 39: | ||
[Zur Kontrolle:<math>f'(x)=\frac{lnx-1}{(ln x)^2}</math>] | [Zur Kontrolle:<math>f'(x)=\frac{lnx-1}{(ln x)^2}</math>] | ||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Infini07-1b.jpg|750px]] | ||
| + | }} | ||
c) Zeigen Sie, dass G<sub>f</sub> einen Wendepunkt W besitzt, und berechnen Sie dessen Koordinaten. | c) Zeigen Sie, dass G<sub>f</sub> einen Wendepunkt W besitzt, und berechnen Sie dessen Koordinaten. | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | [[Bild:Infini07-1c.jpg|750px]] | ||
| + | }} | ||
Version vom 18. Februar 2010, 19:47 Uhr
|
|
1. Gegeben ist die Funktion
b) Bestimmen Sie das Monotonieverhalten von f sowie Art und Lage des Extrempunktes E von Gf .
[Zur Kontrolle:
c) Zeigen Sie, dass Gf einen Wendepunkt W besitzt, und berechnen Sie dessen Koordinaten.
|
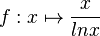mit dem maximalen Definitionsbereich Df = IR+ \ {1}. Der Graph von f wird mit Gf bezeichnet.
]
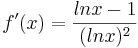