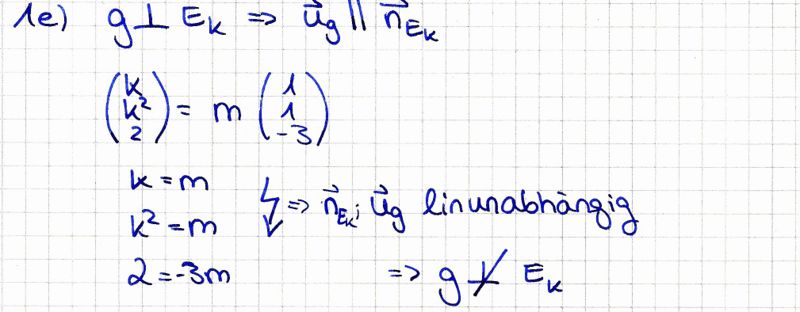2007 V: Unterschied zwischen den Versionen
(Abiaufgabe) |
(Aufgabe_1) |
||
| Zeile 1: | Zeile 1: | ||
| − | __NOTOC__ | + | [[Kategorie:Name der Kategorie]]__NOTOC__ |
<div style="padding:1px;background: #EEEEE6;border:0px groove;"> | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| Zeile 26: | Zeile 26: | ||
Gegeben ist in einem kartesischen Koordinatensystem des IR<sup>3</sup> die Ebenenschar E<sub>k</sub> : k<sup>2</sup>x<sub>1</sub> + k <sup>2</sup>x<sub>2</sub> - k<sup>2</sup> = 0 , mit k ∈ IR als Scharparameter. | Gegeben ist in einem kartesischen Koordinatensystem des IR<sup>3</sup> die Ebenenschar E<sub>k</sub> : k<sup>2</sup>x<sub>1</sub> + k <sup>2</sup>x<sub>2</sub> - k<sup>2</sup> = 0 , mit k ∈ IR als Scharparameter. | ||
<br><br> | <br><br> | ||
| − | |||
| + | '''a)''' Ermitteln Sie, für welche Werte von k die Ebene E<sub>k</sub> den Punkt P(1|2|-3)und zugleich den Punkt Q(0|1|0) enthält. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:Aufgabe_1_a.jpg|800px]] | [[Bild:Aufgabe_1_a.jpg|800px]] | ||
| Zeile 34: | Zeile 34: | ||
<br> | <br> | ||
| − | b) Die beiden Ebenen E<sub>2</sub> und E<sub>-3</sub> schneiden sich in einer Geraden g. Ermitteln Sie eine Gleichung von g in Parameterform und den der beiden Ebenen auf eine Dezimale gerundet. | + | '''b)''' Die beiden Ebenen E<sub>2</sub> und E<sub>-3</sub> schneiden sich in einer Geraden g. Ermitteln Sie eine Gleichung von g in Parameterform und den Schnittwinkel der beiden Ebenen auf eine Dezimale gerundet. |
[mögliches Teilergebnis: g: <math>\vec x = \begin{pmatrix} 1 \\ 2 \\ -3 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 1 \\ 1 \\ -3 \end{pmatrix}</math>, λ ∈ IR ] | [mögliches Teilergebnis: g: <math>\vec x = \begin{pmatrix} 1 \\ 2 \\ -3 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 1 \\ 1 \\ -3 \end{pmatrix}</math>, λ ∈ IR ] | ||
| − | :;1. Lösungsweg: | + | <br><br> |
| + | |||
| + | |||
| + | :;Bestimmung der Gleichung in Parameterform: | ||
| + | |||
| + | :1. Lösungsweg: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:Aufgabe_1_b_Loesung_I.jpg|800px]] | [[Bild:Aufgabe_1_b_Loesung_I.jpg|800px]] | ||
}} | }} | ||
| − | : | + | |
| + | :2. Lösungsweg: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:Aufgabe_1_b_Loesung_II.jpg|800px]] | [[Bild:Aufgabe_1_b_Loesung_II.jpg|800px]] | ||
| + | }} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | :;Berechnung des Schnittwinkels: | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_1_b_Loesung_Winkel.jpg|800px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''c)''' Mit e(k) werde der Betrag des Abstands der Ebene E<sub>k</sub> vom Koordinatenursprung bezeichnet. Zeigen Sie, dass e(k)=<math>\frac{k^2}{\sqrt{k^2+k^4+2}} </math> und dass e(k)<1 ist. | ||
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_1_c.jpg|800px]] | ||
| + | }} | ||
| + | |||
| + | <br /> | ||
| + | '''d)''' Es gibt zwei Scharebenen, deren Schnittwinkel mit der x<sub>3</sub>-Achse 30° besteht. Ermitteln Sie die zugehörigen Werte von k. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_1_d.jpg|800px]] | ||
| + | }} | ||
| + | |||
| + | |||
| + | '''e)''' Untersuchen Sie, ob die Gerade g aus Teilaufgabe 1b senkrecht auf einer Ebene der Schar E<sub>k</sub> steht. | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_1_e.jpg|800px]] | ||
}} | }} | ||
Version vom 17. Februar 2010, 22:02 Uhr
|
|
Gegeben ist in einem kartesischen Koordinatensystem des IR3 die Ebenenschar Ek : k2x1 + k 2x2 - k2 = 0 , mit k ∈ IR als Scharparameter.
a) Ermitteln Sie, für welche Werte von k die Ebene Ek den Punkt P(1|2|-3)und zugleich den Punkt Q(0|1|0) enthält.
b) Die beiden Ebenen E2 und E-3 schneiden sich in einer Geraden g. Ermitteln Sie eine Gleichung von g in Parameterform und den Schnittwinkel der beiden Ebenen auf eine Dezimale gerundet. [mögliches Teilergebnis: g:
|

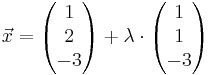 , λ ∈ IR ]
, λ ∈ IR ]



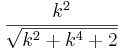 und dass e(k)<1 ist.
und dass e(k)<1 ist.