2009 I: Unterschied zwischen den Versionen
(angelegt) |
|||
| Zeile 42: | Zeile 42: | ||
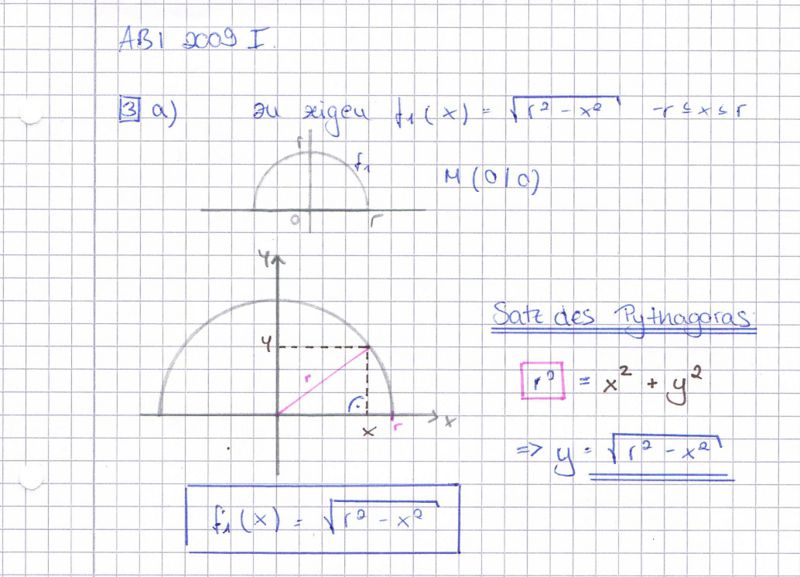
Halbkreis in Bild 1 Graph der Funktion 2 2 | Halbkreis in Bild 1 Graph der Funktion 2 2 | ||
f1 : x a r − x mit | f1 : x a r − x mit | ||
| − | − r ≤ x ≤ r ist. Die Halbkreise der Bilder 2 und 3 sind Graphen der | + | − r ≤ x ≤ r ist. |
| + | |||
| + | :{{Lösung versteckt|1= | ||
| + | |||
| + | [[Bild:ABI_2008_I_A3_1_Lös.jpg|800px]] | ||
| + | |||
| + | |||
| + | Die Halbkreise der Bilder 2 und 3 sind Graphen der | ||
Funktionen f2 und f3 . Geben Sie jeweils Term und Definitionsmenge | Funktionen f2 und f3 . Geben Sie jeweils Term und Definitionsmenge | ||
für f2 und f3 an. | für f2 und f3 an. | ||
Version vom 3. Februar 2010, 17:59 Uhr
Aufgabe 1
Gegeben ist die Schar der Funktionen
a mit k ∈ IR+ und der Definitionsmenge IR . Der Graph von fk wird mit Gk bezeichnet. a) Untersuchen Sie Gk auf Symmetrie und geben Sie das Verhalten von fk für x → −∞ und x → +∞ an.
b) Bestimmen Sie Art und Lage der Extrempunkte von Gk . Die Hochpunkte von Gk bilden den Graphen einer Funktion h. Ermitteln Sie Funktionsterm und Definitionsmenge von h. [Teilergebnis: Hochpunkt bei x = k ] c) Zeigen Sie, dass zwei verschiedene Graphen der Schar nur den Koordinatenursprung gemeinsam haben.
d) Skizzieren Sie unter Verwendung der bisherigen Ergebnisse die Graphen Gk für k = 0,25 und k =1 in ein gemeinsames Koordinatensystem (Längeneinheit 2 cm). Zeichnen Sie auch den Graphen von h ein.
e) Für jedes k begrenzt Gk mit der x-Achse im I. Quadranten ein Flächenstück, das sich ins Unendliche erstreckt. Zeigen Sie, dass dieses Flächenstück keinen endlichen Inhalt besitzt. Für beliebige positive k1, k2 (k1 ≠ k2 ) begrenzen Gk1 und Gk 2im I. Quadranten ein Flächenstück, das sich ebenfalls ins Unendliche erstreckt. Zeigen Sie, dass dieses Flächenstück einen endlichen Inhalt hat, und geben Sie diesen an.
Aufgabe 2
Nun wird die Schar der Funktionen k 2 k x
a für k∈ IR0− betrachtet. Geben Sie die maximale Definitionsmenge Dk von fk in Abhängigkeit von k an. Zeigen Sie, dass an den Definitionslücken Polstellen vorliegen. Hat fk an den Polstellen einen Vorzeichenwechsel? Begründen Sie Ihre Antwort.
Aufgabe 3
a) Die drei folgenden Abbildungen zeigen Halbkreise mit Radius r und Mittelpunkten (0 | 0), (0 | r) und (r | 0) . Begründen Sie, dass der Halbkreis in Bild 1 Graph der Funktion 2 2 f1 : x a r − x mit − r ≤ x ≤ r ist.
- {{Lösung versteckt|1=
Die Halbkreise der Bilder 2 und 3 sind Graphen der
Funktionen f2 und f3 . Geben Sie jeweils Term und Definitionsmenge
für f2 und f3 an.
b) Ein kugelförmiger Tank hat den
Innenradius r und ist mit einer
Flüssigkeit gefüllt. Die Höhe der
eingefüllten Flüssigkeit ist h. Zeigen
Sie mit Hilfe der Integralrechnung,
dass für das Volumen V der
eingefüllten Flüssigkeit gilt:
V (rh h3)
3
= π 2 − 1 .
40