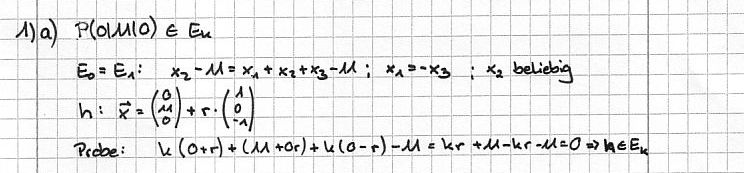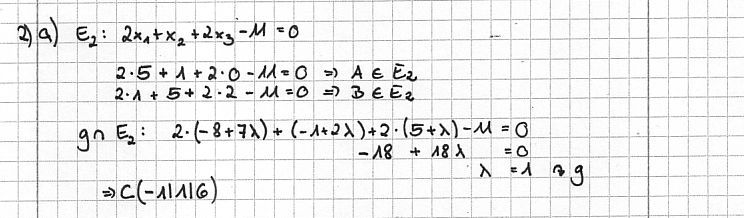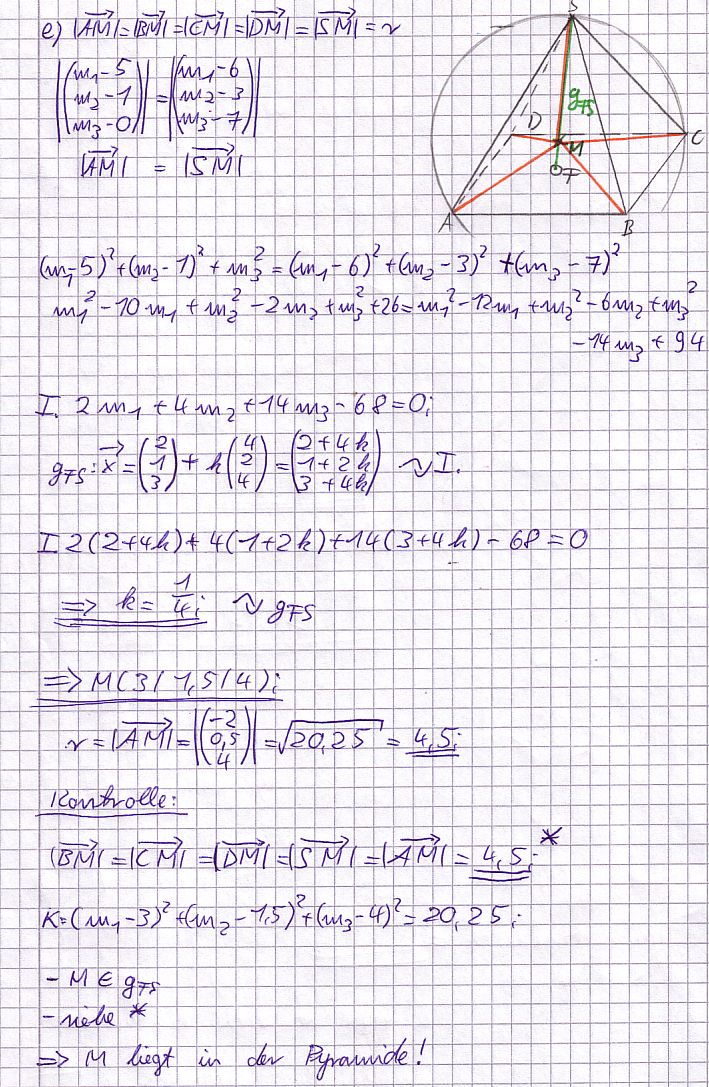2009 V: Unterschied zwischen den Versionen
(layout) |
(Link auf Abituraufgaben) |
||
| Zeile 1: | Zeile 1: | ||
| + | [http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=79e69371e73c4c671417483e9427e728 ''download'' '''Abitur 2009 LK Mathematik Bayern'''] - [[Media:LKM Abi 2009 V lös.doc|Lösung gesamt]] | ||
| + | |||
| + | |||
| + | |||
Gegeben sind in einem kartesischen Koordinatensystem des IR<sup>3</sup> die Punkte A(5|1|0) und B(1|5|2), die Gerade g : <math>\vec x = \begin{pmatrix} -8 \\ -1 \\ 5 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 7 \\ 2 \\ 1 \end{pmatrix}</math>, λ∈ IR sowie die Ebenenschar Ek : kx<sub>1</sub> + x<sub>2</sub> + kx<sub>3</sub> −11 = 0 , k ∈ IR. | Gegeben sind in einem kartesischen Koordinatensystem des IR<sup>3</sup> die Punkte A(5|1|0) und B(1|5|2), die Gerade g : <math>\vec x = \begin{pmatrix} -8 \\ -1 \\ 5 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 7 \\ 2 \\ 1 \end{pmatrix}</math>, λ∈ IR sowie die Ebenenschar Ek : kx<sub>1</sub> + x<sub>2</sub> + kx<sub>3</sub> −11 = 0 , k ∈ IR. | ||
Version vom 2. Februar 2010, 05:56 Uhr
download Abitur 2009 LK Mathematik Bayern - Lösung gesamt
Gegeben sind in einem kartesischen Koordinatensystem des IR3 die Punkte A(5|1|0) und B(1|5|2), die Gerade g :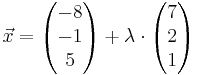 
, λ∈ IR sowie die Ebenenschar Ek : kx1 + x2 + kx3 −11 = 0 , k ∈ IR.
Aufgabe 1
a) Es gibt eine Gerade h, die in allen Ebenen der Schar Ek enthalten ist. Ermitteln Sie eine Gleichung der Geraden h in Parameterform.
b) Weisen Sie nach, dass genau eine Ebene der Schar echt parallel zur Geraden g ist. In welcher Lagebeziehung stehen folglich g und h? Begründen Sie Ihre Antwort.
Aufgabe 2
a) Zeigen Sie, dass die Punkte A und B in der Ebene E2 liegen, und bestimmen Sie die Koordinaten des Schnittpunkts C von E2 mit der Geraden g. [Zur Kontrolle: C(−1|1| 6)]
b) Weisen Sie nach, dass das Dreieck ABC gleichschenklig-rechtwinklig ist, und ermitteln Sie die Koordinaten eines Punkts D so, dass das Viereck ABCD ein Quadrat ist.
Das Quadrat ABCD als Grundfläche bildet zusammen mit einem Punkt S als Spitze eine vierseitige Pyramide ABCDS. Der Punkt S liegt dabei auf der Geraden g und ist so gewählt, dass die Pyramide gerade ist, das heißt, der Fußpunkt F der Pyramidenhöhe ist gleichzeitig der Diagonalenschnittpunkt
des Quadrats.
c) Bestimmen Sie die Koordinaten der Punkte F und S. [Zur Kontrolle: S(6|3|7)]
d) Ermitteln Sie das Volumen der Pyramide sowie den Inhalt ihrer Oberfläche.
e) K sei die Kugel, auf der alle Ecken der Pyramide ABCDS liegen. Bestimmen Sie die Koordinaten des Mittelpunkts M und den Radius r der Kugel K und zeigen Sie, dass M im Inneren der Pyramide liegt.
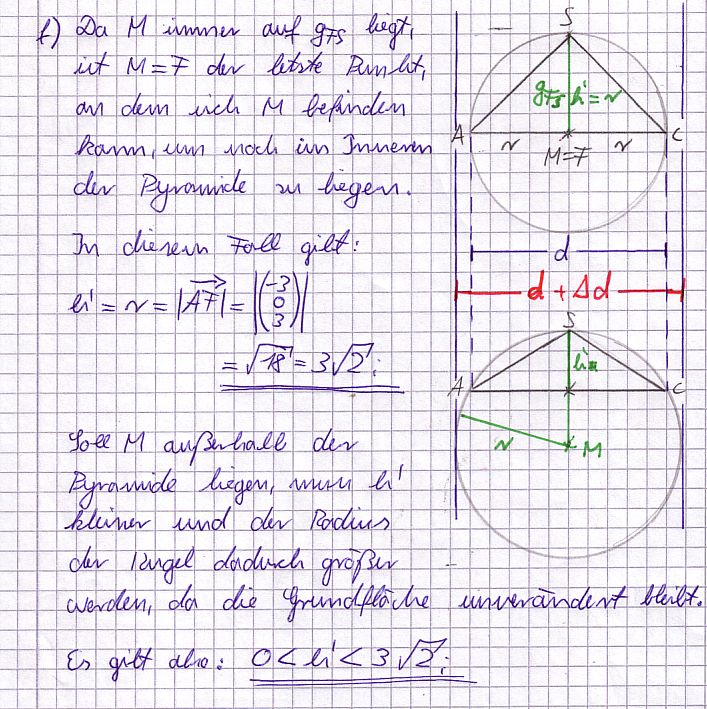
f) Betrachtet werden nun eine gerade Pyramide mit dem Quadrat ABCD als Grundfläche und der Höhe h' > 0 sowie die Kugel durch die Ecken dieser Pyramide. Für welche Werte von h' liegt der Mittelpunkt dieser Kugel außerhalb der Pyramide?
