2009 VI: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 1: | Zeile 1: | ||
'''VI.''' | '''VI.''' | ||
| − | Gegeben sind in einem kartesischen Koordinatensystem des IR<sup>3</sup> die Ebene F, die parallel zur x<sub>3</sub>-Achse ist und die Punkte A(-2/1,5/6) und B(0/3/0) enthält, sowie die Ebenenschar E<sub>a</sub>: 2x<sub>1</sub>+2x<sub>2</sub>+x<sub>3</sub>-a=0 mit a ∈ IR. | + | Gegeben sind in einem kartesischen Koordinatensystem des IR<sup>3</sup> die |
| + | <br />Ebene F, die parallel zur x<sub>3</sub>-Achse ist und die Punkte A(-2/1,5/6) und | ||
| + | <br />B(0/3/0) enthält, sowie die Ebenenschar E<sub>a</sub>: 2x<sub>1</sub>+2x<sub>2</sub>+x<sub>3</sub>-a=0 mit | ||
| + | <br />a ∈ IR. | ||
a) Berechnen Sie eine Gleichung der Ebene F in Normalenform. | a) Berechnen Sie eine Gleichung der Ebene F in Normalenform. | ||
| − | [Zur Kontrolle: F: 3x<sub>1</sub>-4x<sub>2</sub>+12=0 ] | + | <br />[Zur Kontrolle: F: 3x<sub>1</sub>-4x<sub>2</sub>+12=0 ] |
{{Lösung versteckt| | {{Lösung versteckt| | ||
[[Bild:Beispiel.jpg]] | [[Bild:Beispiel.jpg]] | ||
}}<br /> | }}<br /> | ||
| − | b) Die Kugel K mit dem Mittelpunkt M(3/-1/0) berührt die Ebene F. Berechnen Sie die Koordinaten des Berührpunkts und den Radius r der Kugel. | + | b) Die Kugel K mit dem Mittelpunkt M(3/-1/0) berührt die Ebene F. |
| − | [Teilergebnis: r=5 ] | + | <br />Berechnen Sie die Koordinaten des Berührpunkts und den Radius r der Kugel. |
| + | <br />[Teilergebnis: r=5 ] | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
[[Bild:Beispiel.jpg]] | [[Bild:Beispiel.jpg]] | ||
}}<br /> | }}<br /> | ||
| − | c) Die Punktspiegelung der Kugel K am Punkt A ergibt die Kugel K´. Bestimmen Sie die Koordinaten des Mittelpunkts M´ der Kugel K´ und geben Sie deren Radius r´ an. | + | c) Die Punktspiegelung der Kugel K am Punkt A ergibt die Kugel K´. |
| + | <br />Bestimmen Sie die Koordinaten des Mittelpunkts M´ der Kugel K´ und | ||
| + | <br />geben Sie deren Radius r´ an. | ||
<br />[Teilergebnis: M´(-7/4/12)] | <br />[Teilergebnis: M´(-7/4/12)] | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
[[Bild:Beispiel.jpg]] | [[Bild:Beispiel.jpg]] | ||
}}<br /> | }}<br /> | ||
| − | d) Zeigen Sie, dass die Ebenen E<sub>13</sub> und E<sub>-3</sub> symmetrisch bezüglich des Punktes A liegen, und berechnen Sie den Abstand dieser beiden Ebenen. | + | d) Zeigen Sie, dass die Ebenen E<sub>13</sub> und E<sub>-3</sub> symmetrisch bezüglich des |
| + | <br />Punktes A liegen, und berechnen Sie den Abstand dieser beiden Ebenen. | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
[[Bild:Beispiel.jpg]] | [[Bild:Beispiel.jpg]] | ||
}}<br /> | }}<br /> | ||
| − | e) Die Ebene E<sub>13</sub> schneidet die Kugel K in einem Kreis. Berechnen Sie den Mittelpunkt N und den Radius p dieses Kreises. Warum hat der | + | e) Die Ebene E<sub>13</sub> schneidet die Kugel K in einem Kreis. Berechnen Sie den |
| − | [Teilergebnis: N(5/1/1) ] | + | <br />Mittelpunkt N und den Radius p dieses Kreises. Warum hat der Schnitt- |
| + | <br />kreis von E<sub>-3</sub> mit der Kugel K´ ebenfalls den Radius p? | ||
| + | <br />[Teilergebnis: N(5/1/1) ] | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
[[Bild:Beispiel.jpg]] | [[Bild:Beispiel.jpg]] | ||
}}<br /> | }}<br /> | ||
| − | f) Die Kreise aus Teilaufgabe e bilden die Grund- und die Deckfläche eines schiefen Zylinders. Berechnen Sie das Volumen dieses schiefen Zylinders und den Winkel <math>varpi</math> , um den die Zylinderachse gegen die Grundfläche ge-neigt ist. | + | f) Die Kreise aus Teilaufgabe e bilden die Grund- und die Deckfläche eines |
| + | <br />schiefen Zylinders. Berechnen Sie das Volumen dieses schiefen | ||
| + | <br />Zylinders und den Winkel <math>varpi</math> , um den die Zylinderachse gegen die | ||
| + | <br />Grundfläche ge-neigt ist. | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
[[Bild:Beispiel.jpg]] | [[Bild:Beispiel.jpg]] | ||
}}<br /> | }}<br /> | ||
| − | g) In welcher Ebene der Schar E<sub>a</sub> liegt der Punkt M´? Für welche Werte des Scharparameters a schneiden sich die Kugel K´ und die Ebene E<sub>a</sub> in einem Kreis? | + | g) In welcher Ebene der Schar E<sub>a</sub> liegt der Punkt M´? |
| + | <br />Für welche Werte des Scharparameters a schneiden sich die Kugel K´ | ||
| + | <br />und die Ebene E<sub>a</sub> in einem Kreis? | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
[[Bild:Beispiel.jpg]] | [[Bild:Beispiel.jpg]] | ||
}}<br /> | }}<br /> | ||
Version vom 1. Februar 2010, 17:11 Uhr
VI.
Gegeben sind in einem kartesischen Koordinatensystem des IR3 die
Ebene F, die parallel zur x3-Achse ist und die Punkte A(-2/1,5/6) und
B(0/3/0) enthält, sowie die Ebenenschar Ea: 2x1+2x2+x3-a=0 mit
a ∈ IR.
a) Berechnen Sie eine Gleichung der Ebene F in Normalenform.
[Zur Kontrolle: F: 3x1-4x2+12=0 ]
b) Die Kugel K mit dem Mittelpunkt M(3/-1/0) berührt die Ebene F.
Berechnen Sie die Koordinaten des Berührpunkts und den Radius r der Kugel.
[Teilergebnis: r=5 ]
c) Die Punktspiegelung der Kugel K am Punkt A ergibt die Kugel K´.
Bestimmen Sie die Koordinaten des Mittelpunkts M´ der Kugel K´ und
geben Sie deren Radius r´ an.
[Teilergebnis: M´(-7/4/12)]
d) Zeigen Sie, dass die Ebenen E13 und E-3 symmetrisch bezüglich des
Punktes A liegen, und berechnen Sie den Abstand dieser beiden Ebenen.
e) Die Ebene E13 schneidet die Kugel K in einem Kreis. Berechnen Sie den
Mittelpunkt N und den Radius p dieses Kreises. Warum hat der Schnitt-
kreis von E-3 mit der Kugel K´ ebenfalls den Radius p?
[Teilergebnis: N(5/1/1) ]
f) Die Kreise aus Teilaufgabe e bilden die Grund- und die Deckfläche eines
schiefen Zylinders. Berechnen Sie das Volumen dieses schiefen
Zylinders und den Winkel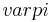 
, um den die Zylinderachse gegen die
Grundfläche ge-neigt ist.
g) In welcher Ebene der Schar Ea liegt der Punkt M´?
Für welche Werte des Scharparameters a schneiden sich die Kugel K´
und die Ebene Ea in einem Kreis?
