Schluss: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Schluss) |
|||
| Zeile 1: | Zeile 1: | ||
==Geschafft !== | ==Geschafft !== | ||
| − | <span style="color: | + | <span style="color: blue">'''Hier bist du nun am Ende der Aufgabe. |
| − | <span style="color: | + | <span style="color: blue">'''Wenn du zu dieser Potenzfunktion noch weitere Aufgaben rechnen möchtest, dann gibt es hier einige Zusätze, was du noch berechnen kannst. |
| − | <span style="color: | + | <span style="color: blue">'''Durch Zusatzaufgaben bekommst du mehr Übung und bist nach einiger Zeit fitter und schneller im Lösen von Potenzfunktionsaufgaben. Des Weiteren sollte man sich bei der Bearbeitung der Aufgaben einen Merkzettel erstellen, um so wichtige Inhalte auf einem Blick festzuhalten wie was am einfachsten errechnet wird, beziehungsweise auf welche verschiedene Weisen man dies tun kann. |
| − | <span style="color: | + | <span style="color: blue">'''Ich hoffe dir hat die interaktive Aufgabe gefallen und du hast dabei etwas gelernt.''' |
Version vom 28. Januar 2010, 17:50 Uhr
Geschafft !
Hier bist du nun am Ende der Aufgabe.
Wenn du zu dieser Potenzfunktion noch weitere Aufgaben rechnen möchtest, dann gibt es hier einige Zusätze, was du noch berechnen kannst.
Durch Zusatzaufgaben bekommst du mehr Übung und bist nach einiger Zeit fitter und schneller im Lösen von Potenzfunktionsaufgaben. Des Weiteren sollte man sich bei der Bearbeitung der Aufgaben einen Merkzettel erstellen, um so wichtige Inhalte auf einem Blick festzuhalten wie was am einfachsten errechnet wird, beziehungsweise auf welche verschiedene Weisen man dies tun kann.
Ich hoffe dir hat die interaktive Aufgabe gefallen und du hast dabei etwas gelernt.
- Mögliche Zusatzaufgaben zur Funktion
- Bestimme die Ortskurve g auf der alle Maxima der Funktion
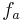 liegen.
liegen.
- [ Ergebnis:
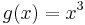 ]
]
- [ Ergebnis:
- Bestimme die Ortskurve g auf der alle Maxima der Funktion
- Bestimme die Ortskurve h auf der alle Wendepunkte der Funktion
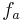 liegen.
liegen.
- [ Ergebnis:
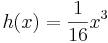 ]
]
- [ Ergebnis:
- Bestimme die Ortskurve h auf der alle Wendepunkte der Funktion
- Überprüfe die Punktsymmetrie für die Funktion
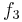 .
.
- [ Ergebnis: f (x0 + x) - y0 = – f(x0 – x) + y [1]
 Punktsymmetrie zum Wendepunkt
Punktsymmetrie zum Wendepunkt 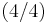 ]
]
- Überprüfe die Punktsymmetrie für die Funktion
Hier geht's zurück zur Übersicht

