weiterführende Aufgaben: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
K
K
Zeile 64: Zeile 64:
  
 
→ Die Länge des Lotes von C auf die Gerade g ist die Höhe h<sub>a</sub>: h<sub>a</sub> <math>=</math> <math>|</math><math>\triangle y</math><math>|</math> <math>=</math> 3 - 1 <math>=</math> 2 (da g parallel zur x-Achse, lässt sich die Länge des Lotes so ohne größere Rechnung bestimmen)<br />
 
→ Die Länge des Lotes von C auf die Gerade g ist die Höhe h<sub>a</sub>: h<sub>a</sub> <math>=</math> <math>|</math><math>\triangle y</math><math>|</math> <math>=</math> 3 - 1 <math>=</math> 2 (da g parallel zur x-Achse, lässt sich die Länge des Lotes so ohne größere Rechnung bestimmen)<br />
 +
 +
(Betrag einer Zahl → [[Digitaler Lernpfad zu linearen Funktionen/Inhaltsverzeichnis/Grundwissensübersicht|Grundwissensübersicht]])
  
 
→ A<sub>D</sub> <math>=</math> <math>\textstyle\frac{1}{2}</math> · 2 · 6 <math>=</math> '''6'''
 
→ A<sub>D</sub> <math>=</math> <math>\textstyle\frac{1}{2}</math> · 2 · 6 <math>=</math> '''6'''

Version vom 27. Januar 2010, 17:49 Uhr

Hier noch ein paar Aufgaben für alle die schon fertig sind, noch üben wollen oder einfach Spaß am rechnen haben. Viele der Aufgaben gehen etwas in die Geometrie über - du wirst sehen, dass man auch hier lineare Gleichungen und Ungleichungen sehr gut gebrauchen kann. Außerdem kannst du prüfen wie gut deine Grundkenntnisse in der Geometrie sitzen!

Die Lösungen zu den weiterführenden Aufgaben sind nicht so ausführlich. Solltest du einen Rechenschritt nicht nachvollziehen können, sieh dir einfach ähnliche Aufgaben in den Arbeitskapiteln vorher noch mal an!
Viel Spaß!:)


Für alle, die dann immer noch nicht genug haben oder zu Hause noch ein bisschen knobeln wollen, gibt es hier noch eine Sammlung an alltagsbezogenen Aufgaben: http://www.brinkmann-du.de/mathe/gost/gr_fkt_01_04.htm



Optional (für den Lehrer): Die Aufgaben können auch an die Schüler verteilt und die Lösung anschließend in kleinen Gruppen der Klasse vorgestellt werden!



1. Berechne a so, dass der Umfang des Grundstücks größer als 100m ist!

a) Weiterf.1a.png b) Weiterf.1b.png c) Weiterf.1c.png

a)
U = 4a
100 < 4a
a > 25

b)
U = 2a + 2·(a + 2) = 2a + 2a + 4 = 4a + 4
100 < 4a + 4
96 < 4a
a > 24

c)
U = 2 + 2a + (a + 2) = 2 + 2a + a + 2 = 4 + 3a
100 < 4 + 3a
96 < 3a
a > 32


2. Werden alle Seiten eines Quadrates um jeweils 4 cm verlängert, so nimmt der Flächeninhalt um weniger als 40cm2 zu. Berechne wie lang die Seiten des Quadrates sein können!

AQ = a2
(a + 4)2 < a2 + 40;
1. binomische Formel anwenden!: a2 + 8a + 16 < a2 + 40
8a + 16 < 40
8a < 24
a < 3 → Die Seiten des Quadrates müssen kürzer als 3 cm sein!


3. Begründe rechnerisch, dass die Punkte A (-1|1); B (5|1) & C (0|3) ein Dreieck bilden und berechne dessen Flächeninhalt!


  • Liegen 3 Punkte nicht alle auf einer Gerade, so bilden sie ein Dreieck!

→ Bilden einer Geraden aus zweien der Punkte: (z.B. A & B)
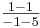
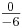
m = \textstyle\frac{1-1}{-1-5} = \textstyle\frac{0}{-6} = 0
y = 0 · x + t; 1 = t; t = 1

→ g: y = 1

→ Prüfen ob der 3. Punkt auf dieser Geraden liegt: (hier C)
3 = 1

→ Da C nicht auf der Geraden durch A & B liegt, bilden die 3 Punkte ein Dreieck!

  • AD 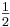= \textstyle\frac{1}{2} · ha · a

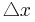
→ A & B bilden die Grundlänge a: a = |\triangle x| = |-1 - 5| = 6

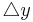
→ Die Länge des Lotes von C auf die Gerade g ist die Höhe ha: ha = |\triangle y| = 3 - 1 = 2 (da g parallel zur x-Achse, lässt sich die Länge des Lotes so ohne größere Rechnung bestimmen)

(Betrag einer Zahl → Grundwissensübersicht)

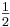→ AD = \textstyle\frac{1}{2} · 2 · 6 = 6


4. Die Gerade h entsteht aus der Geraden g mit der Geradengleichung y = -2x - 3,5 durch Drehung um 90° im Punkt P (1|1,5). Gib die Geradengleichung der Geraden h an und überlege welche Gesetzmäßigkeit sich daraus folgern lässt!
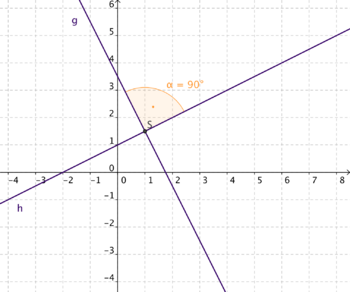
Winkel zwischen Geraden.png

yh = 0,5x + 1
mg & mh betrachten, um mögliche Gesetzmäßigkeit zu vermuten: mg · mh = -2 · 0,5 = -1

→ Tatsächlich gilt folgendes: Sind zwei Geraden zueinander parallel, so ergibt das Produkt ihrer Steigungen -1.
mg · mh = -1


5. Gegeben ist die Gerade g mit der Geradengleichung y = 2x - 1.
a) Berechne die Schnittpunkte mit den Koordinatenachsen!
b) Spiegle die Gerade g an der Winkelhalbierenden des 1. & 3. Quadranten und gib die Gleichung der neuen Geraden h an!
c) Welche Aussage kann man allgemein über einen Punkt machen, der an dieser Winkelhalbierenden gespiegelt wird?
d) Erschließe daraus allgemein die Gleichung einer Geraden, die durch Spiegelung der Geraden y = mx + t an der Winkelhalbierenden des 1. & 3. Quadranten entsteht!

a)
Schnittpunkt mit der x-Achse (Nullstelle): NS (0,5|0)
Schnittstelle mit der y-Achse (y-Abschnitt): Sy (0|-1)
b)
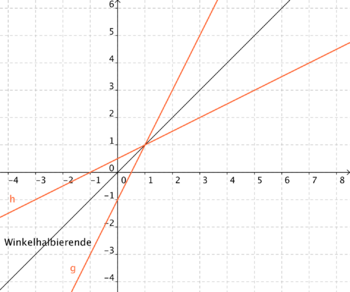
Spiegelung.png
h: y = 0,5x + 0,5
c)
Zwei beliebige Punkte wählen und jeweils deren Spiegelpunkt betrachten: A (3|5) A' (5|3); B (2|3) B' (3|2)
→ Wird ein Punkt an der Winkelhalbierenden des 1. & 3. Quadranten gespiegelt, so werden einfach die Koordinaten getauscht und man erhält den Spiegelpunkt. (Für die Spiegelung an der Winkelhalbierenden des 2. & 4. Quadranten gilt das selbe + jeweils Änderung des Vorzeichens der Koordinaten!)
d)
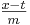
Vertauschen von x & y: x = m · y + t; x - t = m · y; \textstyle\frac{x-t}{m}
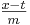
g'; y = \textstyle\frac{x-t}{m}


7. Mario und Christian wohnen in einer Entfernung von 8 km voneinander und gehen sich gleichzeitig entgegen. Mario geht mit einer Geschwindigkeit von 5 km/h, Christian mit 3 km/h.
a) Wie lautet der Zusammenhang zwischen verstrichener Zeit und gegenseitiger Entfernung?
c) Wann treffen sich die beiden?

a)
Mario: y = 5x <br / Christian: y = 3x
→Die Differenz aus 8 km und der Summe der jeweils zurückgelegten Wege ergibt die Entfernung zwischen den beiden: y' = 8 - (3x + 5x) = -8x - 8
b)
→ Die Entfernung ist null für y' = 0: 0 = -8x - 8; x = 1
(Mario: 5 · 1 = 5; Christian: 3 · 1 = 3)

Nach einer Stunde treffen sich Mario & Christian. Mario hat zu diesem Zeitpunkt 5, Christian 3 km zurückgelegt.


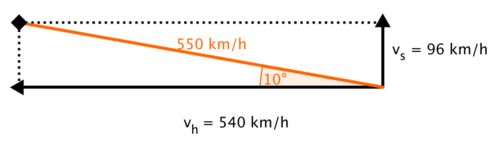
8. Ein Flugzeug befindet sich nach dem Start in einer Höhe von etwa 1000 m Höhe im Steigflug. Der Winkel zur Horizontalen beträgt ungefähr 10° und die momentane Geschwindigkeit 550 km/h

a) Bestimme mit einem Zerlegungsparallelogramm die Geschwindigkeit in horizontaler Richtung und in Steigrichtung!
b) Wie lautet der Zusammenhang zwischen Flughöhe und Zeit?
c) Berechne nach wie vielen Minuten das Flugzeug seine Reisehöhe von 12000 m erreicht hat!
d) Welchen Weg hat das Flugzeug dann in horizontaler Richtung zurückgelegt?

Flugzeug.png




a)
Anhand eines Zerlegungsparallelogramms kann man die gesuchten Längen abmessen. Genauer könnte man sie mit trigonometrischen Gesetzen berechnen, die ihr aber erst in der 9. Klasse lernt.
Parallelogramm2.png

b)
Das Flugzeug steigt pro Stunde um 96 km (a))
→ f(x) = 96x; x ist die Zeit in h

c)
12000 m = 12 km
12 = 96x; x = 0,125 h = 7,5 min
→ Nach 7,5 min hat das Fleugzeug seine Reisehöhe von 12000 m erreicht.

d)
Das Fleuzeug legt 540 km pro Stunde in horizontaler Richtung zurück
540 km · 0,125 h = 67,5 km
→ Es hat nach 7,5 min bereits 67,5 km zurückgelegt.


Von „http://rmg.zum.de/index.php?title=Digitaler_Lernpfad_zu_linearen_Funktionen/Inhaltsverzeichnis/weiterführende_Aufgaben&oldid=28465“