Grundwissensübersicht: Unterschied zwischen den Versionen
K (→Gerade) |
K |
||
| Zeile 4: | Zeile 4: | ||
| − | ==== | + | ==== Abschnittsweise definierte Funktion ==== |
Eine abschnittsweise definierte Funktion hat zwei (oder mehr) verschiedene Funktionsgleichungen für verschiedene Definitionsbereiche. <br /> | Eine abschnittsweise definierte Funktion hat zwei (oder mehr) verschiedene Funktionsgleichungen für verschiedene Definitionsbereiche. <br /> | ||
| Zeile 12: | Zeile 12: | ||
==== Definitionsbereich ==== | ==== Definitionsbereich ==== | ||
| − | Der Definitionsbereich | + | Der Definitionsbereich ist derjenige Bereich, in dem eine Funktion definiert ist.<br /> |
Er gibt also alle x-Werte vor, die in eine Funktionsgleichung eingesetzt werden dürfen. | Er gibt also alle x-Werte vor, die in eine Funktionsgleichung eingesetzt werden dürfen. | ||
| Zeile 28: | Zeile 28: | ||
==== Geradengleichung ==== | ==== Geradengleichung ==== | ||
| − | Eine Geradengleichung legt eine Gerade eindeutig fest.<br /> | + | Eine Geradengleichung ist die Funktionsvorschrift zu einer linearen Funktion und legt eine Gerade eindeutig fest.<br /> |
y = mx + t<br /> | y = mx + t<br /> | ||
| − | m ist die Steigung, t ist der y-Abschnitt | + | m ist die Steigung, t ist der y-Abschnitt. |
==== Graph ==== | ==== Graph ==== | ||
Ein Graph ist die zeichnerische Darstellung einer Funktion. | Ein Graph ist die zeichnerische Darstellung einer Funktion. | ||
| − | ==== | + | ==== Linearer Zusammenhang ==== |
siehe Proportionalität | siehe Proportionalität | ||
==== Proportionalität ==== | ==== Proportionalität ==== | ||
| − | + | Ein proportionaler Zusammenhang liegt dann vor, wenn sich zwei Größen zueinander proportional verhalten. Das heißt sie steigen bzw. fallen im gleichen Verhältnis und haben somit immer einen konstanten Quotienten q = \frac{2.\;Gr \ddot osse}{1.\;Gr \ddot osse} . (verdoppelt sich z.B. der Wert der x-Koordinate, so verdopplet sich auch der Wert der y-Koordinate) | |
| − | Dies nennt man dann auch einen linearen Zusammenhang, den man mit einer linearen Funktion beschreiben kann. Ihr | + | Dies nennt man dann auch einen linearen Zusammenhang, den man mit einer linearen Funktion beschreiben kann. Ihr Graph ist eine Gerade. |
==== Schnittpunkt ==== | ==== Schnittpunkt ==== | ||
| − | Der Schnittpunkt zweier | + | Der Schnittpunkt zweier Graphen ist die Stelle, an der beide denselben x- und y-Wert besitzen.<br /> |
Zur Berechnung werden die beiden Funktionsgleichungen gleichgesetzt und nach x aufgelöst. | Zur Berechnung werden die beiden Funktionsgleichungen gleichgesetzt und nach x aufgelöst. | ||
==== Steigung m ==== | ==== Steigung m ==== | ||
| − | Die Steigung m einer Geraden sagt aus ob diese steigt (positives m) oder fällt (negatives m) und außerdem wie steil sie das tut.<br /> | + | Die Steigung m einer Geraden sagt aus, ob diese steigt (positives m) oder fällt (negatives m) und außerdem wie steil sie das tut.<br /> |
m = <math>\frac{\triangle y}{\triangle x}</math> | m = <math>\frac{\triangle y}{\triangle x}</math> | ||
==== Ungleichheitszeichen ==== | ==== Ungleichheitszeichen ==== | ||
| − | Es gibt | + | Es gibt vier verschiedene Ungleichheitszeichen: > <small>(größer)</small> < <small>(kleiner)</small> <math>\ge</math> <small>(größer gleich)</small> <math>\le</math> <small>(kleiner gleich)</small> |
==== Ungleichung ==== | ==== Ungleichung ==== | ||
Eine Ungleichung besteht aus zwei Termen, die durch ein Ungleichheitszeichen verbunden sind. <br /> | Eine Ungleichung besteht aus zwei Termen, die durch ein Ungleichheitszeichen verbunden sind. <br /> | ||
| − | Es gelten dieselben Äquivalenzumformungen wie bei Gleichungen außer: beim Multiplizieren oder Dividieren einer negativen Zahl (Term) wir das Ungleichheitszeichen umgedreht! | + | Es gelten dieselben Äquivalenzumformungen wie bei Gleichungen, außer: beim Multiplizieren oder Dividieren einer negativen Zahl (Term) wir das Ungleichheitszeichen umgedreht! |
==== Wertebereich ==== | ==== Wertebereich ==== | ||
| − | Der Wertebereich ist die Menge aller derjenigen y-Werten, die eine Funktion annehmen kann. Bei einer linearen Funktion ist der Wertebereich unendlich | + | Der Wertebereich ist die Menge aller derjenigen y-Werten, die eine Funktion annehmen kann. Bei einer linearen Funktion ist der Wertebereich unendlich. Sie kann alle y-Werte annehmen - ihr Graph steigt und fällt unendlich. |
==== y-Abschnitt t ==== | ==== y-Abschnitt t ==== | ||
Aktuelle Version vom 27. Januar 2010, 17:45 Uhr
Diese kleine Übersicht dient als "Nachschlagewerk" zu den wichtigsten Begriffen rund um lineare Funktionen...
Abschnittsweise definierte Funktion
Eine abschnittsweise definierte Funktion hat zwei (oder mehr) verschiedene Funktionsgleichungen für verschiedene Definitionsbereiche.
Betragsstriche
Auf der Zahlengeraden bedeutet der Betrag einer Zahl den Abstand von der Null.
Ist eine negative Zahl in Betragsstriche gesetzt, so wird das "-" ignoriert. Ein Betrag ist immer positiv!
Definitionsbereich
Der Definitionsbereich ist derjenige Bereich, in dem eine Funktion definiert ist.
Er gibt also alle x-Werte vor, die in eine Funktionsgleichung eingesetzt werden dürfen.
Funktionsgleichung
Die Funktionsgleichung ist eine Funktionsvorschrift. Sie legt eine Funktion fest. f(x) = ...
Funktionswert
Der Funktionswert ist der zu einem bestimmten x zugehörige y-Wert.
Zur Berechnung wird x-Wert eingesetzt.
Gerade
Eine Gerade ist eine theoretisch unendlich lange und unendlich dünne Linie.
Für jede Gerade gibt es eine Geradengleichung, die diese eindeutig festlegt.
Sie ist der Graph einer linearen Funktion.
Geradengleichung
Eine Geradengleichung ist die Funktionsvorschrift zu einer linearen Funktion und legt eine Gerade eindeutig fest.
y = mx + t
m ist die Steigung, t ist der y-Abschnitt.
Graph
Ein Graph ist die zeichnerische Darstellung einer Funktion.
Linearer Zusammenhang
siehe Proportionalität
Proportionalität
Ein proportionaler Zusammenhang liegt dann vor, wenn sich zwei Größen zueinander proportional verhalten. Das heißt sie steigen bzw. fallen im gleichen Verhältnis und haben somit immer einen konstanten Quotienten q = \frac{2.\;Gr \ddot osse}{1.\;Gr \ddot osse} . (verdoppelt sich z.B. der Wert der x-Koordinate, so verdopplet sich auch der Wert der y-Koordinate) Dies nennt man dann auch einen linearen Zusammenhang, den man mit einer linearen Funktion beschreiben kann. Ihr Graph ist eine Gerade.
Schnittpunkt
Der Schnittpunkt zweier Graphen ist die Stelle, an der beide denselben x- und y-Wert besitzen.
Zur Berechnung werden die beiden Funktionsgleichungen gleichgesetzt und nach x aufgelöst.
Steigung m
Die Steigung m einer Geraden sagt aus, ob diese steigt (positives m) oder fällt (negatives m) und außerdem wie steil sie das tut.
m =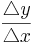 
Ungleichheitszeichen
Es gibt vier verschiedene Ungleichheitszeichen: > (größer) < (kleiner)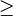 
(größer gleich) 
(kleiner gleich)
Ungleichung
Eine Ungleichung besteht aus zwei Termen, die durch ein Ungleichheitszeichen verbunden sind.
Es gelten dieselben Äquivalenzumformungen wie bei Gleichungen, außer: beim Multiplizieren oder Dividieren einer negativen Zahl (Term) wir das Ungleichheitszeichen umgedreht!
Wertebereich
Der Wertebereich ist die Menge aller derjenigen y-Werten, die eine Funktion annehmen kann. Bei einer linearen Funktion ist der Wertebereich unendlich. Sie kann alle y-Werte annehmen - ihr Graph steigt und fällt unendlich.
y-Abschnitt t
Der y-Abschnitt ist diejenige Stelle, an der eine Gerade die y-Achse schneidet.
Links
Unter folgenden Links findest du nützliche Grundwissensübersichten zum Stoff der gesamten 8. Klasse:
http://www.khg-online.de/unterricht/faecher/mathematik/grundwissen.htm
http://www.cjt-gym-lauf.de/Faecher/Mathematik/Grundwissen/Grundwissen8A.htm
