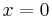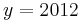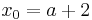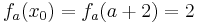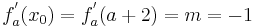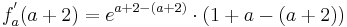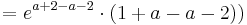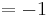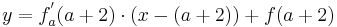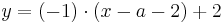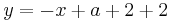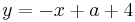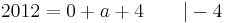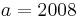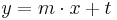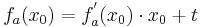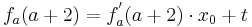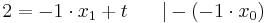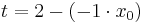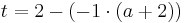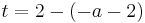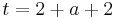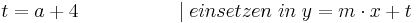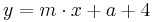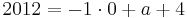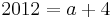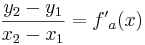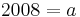Lösung von Teilaufgabe c) 1.: Unterschied zwischen den Versionen

Version vom 26. Januar 2010, 17:39 Uhr

Inhaltsverzeichnis

1 Tangente im Punkt W_a( a + 2 / 2 ) an G_{f_a} mit dem Schnittpunkt A (0 / 2012 )

Tangente im Punkt W_a( a + 2 / 2 ) an G_{f_a} mit dem Schnittpunkt A (0 / 2012 )

Wichtig für diese Aufgabe ist, dass man aus den gegebenen Größen, die richtigen Schlussfolgerungen zieht:

$mit:\;$

$x = 0\;$

$y = 2012\;$

$x_0 = a + 2\;$

$f_a( x_0 ) = f_a( a + 2 ) = 2\;$

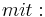
Egal für welchen Lösungsweg man sich entscheidet, die Steigung am Punkt W_a( a + 2 / 2 ) wird in jedem Fall benötigt. Um diese zu erhalten, braucht man nur die x-Koordinaten des Punktes in die erste Ableitung einsetzen.

$f^{'}_a( x_0 ) = f^{'}_a( a + 2 ) = m = -1\;$

$f^{'}_a( a + 2 ) = e^{a + 2 - ( a + 2 )}\cdot ( 1 + a - ( a + 2 ) )$

$= e^{a + 2 - a - 2 }\cdot ( 1 + a - a - 2 ) )$

$= e^{0}\cdot ( -1 ) )$

$= -1\;$

Lösung; Tangentengleichung

Tangentengleichung: siehe Formelsammlung Seite 58

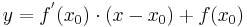
$y = f^{'}( x_0 )\cdot ( x - x_0 ) + f ( x_0)$

$y = f^{'}_a( a + 2 )\cdot ( x - ( a + 2 )) + f ( a + 2 )$

$y = (-1)\cdot ( x - a - 2 ) + 2$

$y = -x + a + 2 + 2\;$

$y = -x + a + 4\;$

$2012 = 0 + a + 4\;\;\;\;\;\;\; | -4$

$a = 2008\;$

Lösung; Fußweg

$y = m\cdot x + t$

$f_a( x_0 ) = f^{'}_a( x_0 )\cdot x_0 + t$

$f_a( a + 2 ) = f^{'}_a( a + 2 )\cdot x_0 + t$

$2 = -1\cdot x_1 + t \;\;\;\;\;\; | - ( -1\cdot x_0)$

$t = 2 - ( -1\cdot x_0 )$

$t = 2 - ( -1\cdot ( a + 2 ))$

$t = 2 - ( -a - 2)\;$

$t = 2 + a + 2 \;$

$t = a + 4 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; |\;einsetzen\; in\; y = m\cdot x + t$

$y = m\cdot x + a + 4$

$2012 = -1\cdot 0 + a + 4$

$2012 = a + 4 \;$

$a = 2008\;$

Lösung; Clever

$\frac{y_2 - y_1}{x_2 - x_1} = f{'}_a ( x )$

$\frac{2012 - 2}{0 - ( a + 2 )} = -1$

$\frac{2010}{(-a - 2 )} = -1 \;\;\;\;\;\;\;\;\;\;| \cdot( -a - 2 )$

$2010 = a + 2\;$

$2008 = a\;$

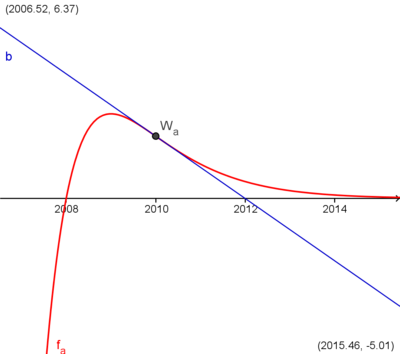
Verdeutlichung durch Grafiken

Zuerst, das Bild, auf dem sowohl die Tangente an den Wendepunkt des Graphens 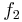$f_2\,$ als auch der Schnittpunkt mit der y-Achse bei 2012 zu sehen ist.
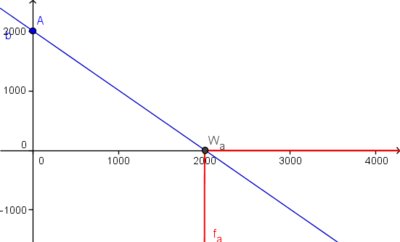
Als zweites Bild zunächst einen Zoom auf den Schnittpunkt mit der y-Achse,
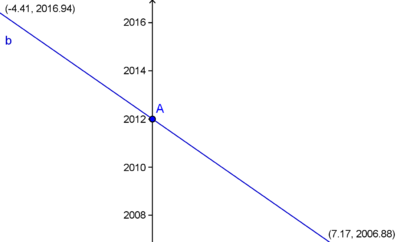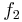und als drittes Bild ein Zoom auf den Graphen von $f_2\,$ .

@@ Zeile 1: / Zeile 1: @@
 == Tangente im Punkt W<sub>a</sub>( a + 2 / 2 ) an G<sub>f<sub>a</sub></sub> mit dem Schnittpunkt A (0 / 2012 ) ==
+Wichtig für diese Aufgabe ist, dass man aus den gegebenen Größen, die richtigen Schlussfolgerungen zieht:
 <math>mit:\;</math><br />
@@ Zeile 7: / Zeile 9: @@
 :<math>x_0 = a + 2\;</math><br />
 :<math>f_a( x_0 ) = f_a( a + 2 ) = 2\;</math><br />
+Egal für welchen Lösungsweg man sich entscheidet, die Steigung am Punkt W<sub>a</sub>( a + 2 / 2 ) wird in jedem Fall benötigt.
+Um diese zu erhalten, braucht man nur die x-Koordinaten des Punktes in die erste Ableitung einsetzen.
 :<math>f^{'}_a( x_0 ) = f^{'}_a( a + 2 ) = m = -1\;</math><br />

Lösung von Teilaufgabe c) 1.: Unterschied zwischen den Versionen

Version vom 26. Januar 2010, 17:39 Uhr

Inhaltsverzeichnis