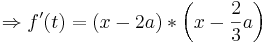Extremwerte: Unterschied zwischen den Versionen
K |
|||
| Zeile 1: | Zeile 1: | ||
===Bestimmung der maximalen und minimalen Volumina=== | ===Bestimmung der maximalen und minimalen Volumina=== | ||
| − | '''''<span style="color: darkorange">Es soll | + | '''''<span style="color: darkorange">Es soll in Abhängigkeit von a ermittelt werden, zu welchen Zeitpunkten t ein relatives Maximum bzw. Minimum vorliegt. Diese Funktionswerte sollen berechnet werden.</span> |
{| | {| | ||
|width=400px| | |width=400px| | ||
| − | ''Maxima und Minima sind Punkte auf | + | ''Maxima und Minima sind Punkte auf einem Graphen, die in ihrem im Umkreis die höchsten beziehungsweise tiefsten Punkte auf dem Graphen sind. An den Extrempunkten besitzt die Funktion eine waagrechte Tangente, dass heißt, die Steigung ist Null. |
:Um diese Extremwerte einer Funktion zu errechnen, wird die erste Ableitung benötigt.'' | :Um diese Extremwerte einer Funktion zu errechnen, wird die erste Ableitung benötigt.'' | ||
| Zeile 41: | Zeile 41: | ||
|width=15px| | |width=15px| | ||
|valign="top" | | |valign="top" | | ||
| − | Jeder Graph G<sub>a</sub> besitzt '''zwei Extremwerte'''. In der Funktion f<sub>3</sub> sind es die unten eingezeichneten Punkte. Man sieht deutlich, dass '''an der Stelle, an der die Ableitung '''(blaue Funktion)''' gleich Null wird, die Extremwerte | + | Jeder Graph G<sub>a</sub> besitzt '''zwei Extremwerte'''. In der Funktion f<sub>3</sub> sind es die unten eingezeichneten Punkte. Man sieht deutlich, dass '''an der Stelle, an der die Ableitung '''(blaue Funktion)''' gleich Null wird, die Extremwerte und die waagrechten Tangenten liegen''' (rot eingezeichnet). |
:<ggb_applet width="376" height="411" version="3.2" ggbBase64="UEsDBBQACAAIADWlNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVhNb+M2ED13fwWh026L2KJkyRZgZ5Gme1gg2xRw20MPBWiJltlIoitSiZxf3+GHbMteO5Kz6V4sihySM2/ePNKafqzzDD3SUjBezBw8cB1Ei5gnrEhnTiWXVxPn4/W7aUp5ShclQUte5kTOHH/gOaq/YtfvfpiKFX9CJNMmfzL6NHOWJBPUQWJdUpKIFaWy1U+qmmWMlJv7xT80lmI3YBb5XKwr2EWWFfTFeXLHRPM6VBsueSEREuyZgtOe6psOtS9TWsUZSxgp1H7aNzBC6IklcgVuj0MHrShLV7DcyI3MajHnZTLfCElzVP9FSw5jk8HIH42DcIJ9b4wDz0EbM+JFeOBhz3dDd4SDcDyBKGOSgSO+O/AjD0fuKAijSM2GSafH9Nb0cU6lBLQFIjUVTchpyZL99mfxM8+SLUprzgp5S9ayKnWifNs1lxu1GSSxVCHeFGlGbR8EEK9o/LDg9dzA5pulf9+s9RTtziK95RkvUQkTAnA/tc+FeWob5efWytU2rrawa6hFt+M48rSFfi7MU1tlrDCu2bj9JmjsNtswgVQHLK741cCRkQXNZo6DqoLJu+ZFsvjBRoqN/a9VvgBeN9OUwS/AIlLE1BC9vQt+u12mwwNSTh9oWdDMUK+A7Fe8EuiRZE2CtWsJjVkOr2bAwkZUSv8An0xvQtOSWntbOgZUPeru0/ugezpsnFA+CHA/lqABEIFU4akSlSteqlZCpOpRxZXRnELlSc2ZosppyeItWMRRu8EWld3Ib1DW+sB1qW85bCftahrGT9AKVGG9ItAaYEsesqFlK0a92hee2J2tnQDUwTBnjbblpJ45oWqRheBZJek8BgCLOx4TqSXQ5NHKBXZdZQtzxhPV2EBMnmosWU135Qg4sWdIJGnFs2O4XAEtCiqELkO5X3CkgBxr4EF91tZLsaZqdd1urNEagtbFvqUI8MrkQ2WmBqUVSsUbYJeg5DWsuHxff0AzBIuhIRrB74+o/vs9pOYDukLEvHnq7SdEbAv6HDQ8yveyKjRHnN0WJ+MMDuJsMaBVYv0I4HYkgHsmB23f9lGMeZ6TIkEFyWH4NyWpOkSmjiNEXBWycbWSTc8ne/zYuUeoaWHeRvvJcy6BoxHjvoDcL5eCSk1gzd6r4Fy5aFabnp0bWj2EWsKzJaBL4XlPRM3Zo85ZPXe033skO69EG/dCG38ntHFk4PZeAXdo4Xa7wH1eC1KrBanRAr+tBZ7RAk+/a0XYaUEnHUg76AAOXhKCvaPvlBJ47uhyLfgq3F2c7sfZ9IizN30oe/MCY0+ghD1DWf20t7WLkTo8lNS52/VQ+ppgvMRg/4jBZ+8Zi8N7htfhntGBXa+4aLwGsdOBK3JuA4hPF5nfrO9939P2BUHDB3S42uatW1T038IYCXMFZ/k6YzGTPUBMvgmIPbn0xiiG/weKbZG6vUykWlL+ZgLVWZ6u8CAI3XEwGk8i+DsfehrX8SAKoyAY+5MoCP0oDPpJV/uAuC/hT1TKC5LdKRq2Twq4CyKCVWUfnhj0/InRojTtQGn/UkpfehM6ytgOddfyFzf8nXTjr9+Tv30SgU0ikqNErHokYtXhFvTqRGDXfkdRz2+fDPdsLo7C6JqL4f4nBv2tzn5PvP4PUEsHCFnFJRrIBAAAgRQAAFBLAQIUABQACAAIADWlNzxZxSUayAQAAIEUAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAAgUAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | :<ggb_applet width="376" height="411" version="3.2" ggbBase64="UEsDBBQACAAIADWlNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVhNb+M2ED13fwWh026L2KJkyRZgZ5Gme1gg2xRw20MPBWiJltlIoitSiZxf3+GHbMteO5Kz6V4sihySM2/ePNKafqzzDD3SUjBezBw8cB1Ei5gnrEhnTiWXVxPn4/W7aUp5ShclQUte5kTOHH/gOaq/YtfvfpiKFX9CJNMmfzL6NHOWJBPUQWJdUpKIFaWy1U+qmmWMlJv7xT80lmI3YBb5XKwr2EWWFfTFeXLHRPM6VBsueSEREuyZgtOe6psOtS9TWsUZSxgp1H7aNzBC6IklcgVuj0MHrShLV7DcyI3MajHnZTLfCElzVP9FSw5jk8HIH42DcIJ9b4wDz0EbM+JFeOBhz3dDd4SDcDyBKGOSgSO+O/AjD0fuKAijSM2GSafH9Nb0cU6lBLQFIjUVTchpyZL99mfxM8+SLUprzgp5S9ayKnWifNs1lxu1GSSxVCHeFGlGbR8EEK9o/LDg9dzA5pulf9+s9RTtziK95RkvUQkTAnA/tc+FeWob5efWytU2rrawa6hFt+M48rSFfi7MU1tlrDCu2bj9JmjsNtswgVQHLK741cCRkQXNZo6DqoLJu+ZFsvjBRoqN/a9VvgBeN9OUwS/AIlLE1BC9vQt+u12mwwNSTh9oWdDMUK+A7Fe8EuiRZE2CtWsJjVkOr2bAwkZUSv8An0xvQtOSWntbOgZUPeru0/ugezpsnFA+CHA/lqABEIFU4akSlSteqlZCpOpRxZXRnELlSc2ZosppyeItWMRRu8EWld3Ib1DW+sB1qW85bCftahrGT9AKVGG9ItAaYEsesqFlK0a92hee2J2tnQDUwTBnjbblpJ45oWqRheBZJek8BgCLOx4TqSXQ5NHKBXZdZQtzxhPV2EBMnmosWU135Qg4sWdIJGnFs2O4XAEtCiqELkO5X3CkgBxr4EF91tZLsaZqdd1urNEagtbFvqUI8MrkQ2WmBqUVSsUbYJeg5DWsuHxff0AzBIuhIRrB74+o/vs9pOYDukLEvHnq7SdEbAv6HDQ8yveyKjRHnN0WJ+MMDuJsMaBVYv0I4HYkgHsmB23f9lGMeZ6TIkEFyWH4NyWpOkSmjiNEXBWycbWSTc8ne/zYuUeoaWHeRvvJcy6BoxHjvoDcL5eCSk1gzd6r4Fy5aFabnp0bWj2EWsKzJaBL4XlPRM3Zo85ZPXe033skO69EG/dCG38ntHFk4PZeAXdo4Xa7wH1eC1KrBanRAr+tBZ7RAk+/a0XYaUEnHUg76AAOXhKCvaPvlBJ47uhyLfgq3F2c7sfZ9IizN30oe/MCY0+ghD1DWf20t7WLkTo8lNS52/VQ+ppgvMRg/4jBZ+8Zi8N7htfhntGBXa+4aLwGsdOBK3JuA4hPF5nfrO9939P2BUHDB3S42uatW1T038IYCXMFZ/k6YzGTPUBMvgmIPbn0xiiG/weKbZG6vUykWlL+ZgLVWZ6u8CAI3XEwGk8i+DsfehrX8SAKoyAY+5MoCP0oDPpJV/uAuC/hT1TKC5LdKRq2Twq4CyKCVWUfnhj0/InRojTtQGn/UkpfehM6ytgOddfyFzf8nXTjr9+Tv30SgU0ikqNErHokYtXhFvTqRGDXfkdRz2+fDPdsLo7C6JqL4f4nBv2tzn5PvP4PUEsHCFnFJRrIBAAAgRQAAFBLAQIUABQACAAIADWlNzxZxSUayAQAAIEUAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAAgUAAAAA" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | ||
|} | |} | ||
| Zeile 48: | Zeile 48: | ||
| − | ''Man hat nun die Werte in Abhängigkeit von a ermittelt, an denen die Funktion eine waagrechte Tangente besitzt. Um nun zu prüfen, ob es sich dabei um einen Extrempunkt handelt und | + | ''Man hat nun die Werte in Abhängigkeit von a ermittelt, an denen die Funktion eine waagrechte Tangente besitzt. Um nun zu prüfen, ob es sich dabei um einen Extrempunkt handelt und welcher Art dieser Extremwert ist, kann man hier anhand verschiedener Lösungen vorgehen.'' |
{| | {| | ||
| Zeile 61: | Zeile 61: | ||
::<math>\Rightarrow</math> relatives Minimum | ::<math>\Rightarrow</math> relatives Minimum | ||
| − | ::Wäre die zweite Ableitung ''gleich Null'', handelt es sich bei dem | + | ::Wäre die zweite Ableitung ''gleich Null'', handelt es sich bei dem Punkt um einen ''Terassenpunkt'', dass heißt, dass die Steigung der Funktion ''keinen Vorzeichenwechsel an dieser Stelle'' hat, aber jedoch eine waagrechte Tangente. Bei solche einem Punkt handelt es sich um '''keinen Extremwert'''. |
| − | ::''<span style="color: darkblue">Gib mit dieser Lösungsmöglichkeit die Art der Extremwerte.</span> | + | ::''<span style="color: darkblue">Gib mit dieser Lösungsmöglichkeit die Art der Extremwerte an.</span> |
::{{Lösung versteckt|1= | ::{{Lösung versteckt|1= | ||
| Zeile 98: | Zeile 98: | ||
::<math>\lim_{h\to0} f '(\frac{2}{3}a - h)> 0</math> und <math>\lim_{h\to0} f '(\frac{2}{3}a + h)< 0</math> | ::<math>\lim_{h\to0} f '(\frac{2}{3}a - h)> 0</math> und <math>\lim_{h\to0} f '(\frac{2}{3}a + h)< 0</math> | ||
| − | ::Graphische | + | ::Graphische Vorstellung: |
::<math> \Rightarrow E_1\left( 2a / 0 \right)</math> '''ist Minimum, | ::<math> \Rightarrow E_1\left( 2a / 0 \right)</math> '''ist Minimum, | ||
::* da links von t = 2a der Graph fällt. | ::* da links von t = 2a der Graph fällt. | ||
| Zeile 119: | Zeile 119: | ||
::<math>f '(t)= \left( x - t_1 \right) * \left( x - t_2 \right)</math>, | ::<math>f '(t)= \left( x - t_1 \right) * \left( x - t_2 \right)</math>, | ||
| − | :geschrieben werden. Hier sind die Werte t<sub>1</sub> und t<sub>2</sub> die errechneten t - Werte, bei | + | :geschrieben werden. Hier sind die Werte t<sub>1</sub> und t<sub>2</sub> die errechneten t - Werte, bei welchen die erste Ableitung Null wird. |
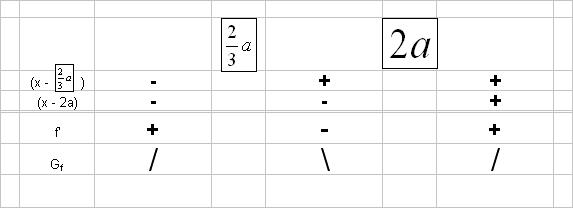
| − | :Man stellt eine Vorzeichentabelle für jeden Faktor auf und erhält durch | + | :Man stellt eine Vorzeichentabelle für jeden Faktor auf und erhält durch Multiplikation der Vorzeichen das Monotonieverhalten und dadurch die Arten der Extremwerte. |
::<span style="color: darkblue">Erstelle mit Hilfe des umgeformten Ableitungsproduktes eine Vorzeichentabelle und vergleiche sie mit dem rechts gezeigten Monotonieverhalten.</span> | ::<span style="color: darkblue">Erstelle mit Hilfe des umgeformten Ableitungsproduktes eine Vorzeichentabelle und vergleiche sie mit dem rechts gezeigten Monotonieverhalten.</span> | ||
| Zeile 129: | Zeile 129: | ||
:: | :: | ||
| − | [[Bild: | + | [[Bild:Vorzeichentabelle neu.jpg]] |
::<u><span style="color: red">'''Merke:'''</span></u> Durch das Aufstellen einer Vorzeichentabelle erhält man das Monotonieverhalten des Graphen und kann sich somit die Art der Extremwerte erschließen. | ::<u><span style="color: red">'''Merke:'''</span></u> Durch das Aufstellen einer Vorzeichentabelle erhält man das Monotonieverhalten des Graphen und kann sich somit die Art der Extremwerte erschließen. | ||
}} | }} | ||
Version vom 25. Januar 2010, 22:54 Uhr
Bestimmung der maximalen und minimalen Volumina
Es soll in Abhängigkeit von a ermittelt werden, zu welchen Zeitpunkten t ein relatives Maximum bzw. Minimum vorliegt. Diese Funktionswerte sollen berechnet werden.
|
Maxima und Minima sind Punkte auf einem Graphen, die in ihrem im Umkreis die höchsten beziehungsweise tiefsten Punkte auf dem Graphen sind. An den Extrempunkten besitzt die Funktion eine waagrechte Tangente, dass heißt, die Steigung ist Null.
|
Jeder Graph Ga besitzt zwei Extremwerte. In der Funktion f3 sind es die unten eingezeichneten Punkte. Man sieht deutlich, dass an der Stelle, an der die Ableitung (blaue Funktion) gleich Null wird, die Extremwerte und die waagrechten Tangenten liegen (rot eingezeichnet). |
Man hat nun die Werte in Abhängigkeit von a ermittelt, an denen die Funktion eine waagrechte Tangente besitzt. Um nun zu prüfen, ob es sich dabei um einen Extrempunkt handelt und welcher Art dieser Extremwert ist, kann man hier anhand verschiedener Lösungen vorgehen.
|
|
- Lösung 3: Vorzeichentabelle
|
|
Hier geht's zur Aufgabe: Bestimmung der größten Senkung der Durchflussgeschwindigkeit
 n-1
n-1
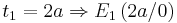
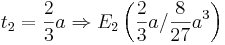
 Rechtskrümmung bzw Rechtskurve
Rechtskrümmung bzw Rechtskurve
 relatives Maximum
relatives Maximum
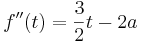
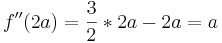
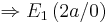 ist Minimum
ist Minimum
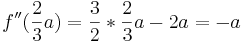
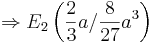 ist Maximum
ist Maximum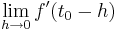
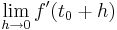 ein.
ein.
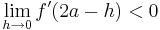 und
und 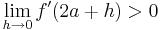
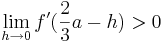 und
und 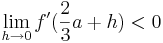
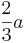 der Graph steigt.
der Graph steigt.
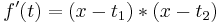 ,
,