Wendepunkt: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Aufgabe: Wendepunkt) |
|||
| Zeile 1: | Zeile 1: | ||
| − | === | + | ===Bestimmung der größten Senkung der Durchflussgeschwindigkeit=== |
'''''<span style="color: darkorange">Es soll, in Abhängigkeit von a bestimmt werden, wann die Druchflussgeschwindigkeit besonders stark absinkt. Dieser Wert soll zum Zeitpunkt t berechnet werden.</span> | '''''<span style="color: darkorange">Es soll, in Abhängigkeit von a bestimmt werden, wann die Druchflussgeschwindigkeit besonders stark absinkt. Dieser Wert soll zum Zeitpunkt t berechnet werden.</span> | ||
| Zeile 12: | Zeile 12: | ||
| − | :''An dem erhaltenem Punkt besitzt der Graph G<sub>f</sub> den größten negativen Steigungswert. Dieser Punkt | + | :''An dem erhaltenem Punkt besitzt der Graph G<sub>f</sub> den größten negativen Steigungswert. Dieser Punkt ist ein möglicher Wendepunkt. An ihm ändert der Graph sein Krümmungsverhalten.'' |
| + | |||
| + | ::<span style="color: darkblue">Errechne die Koordinaten des möglichen Wendepunktes und überprüfe, ob es einer ist.</span> | ||
| + | |||
| + | ::'''<u><span style="color: red">Merke:</span></u>''' Es handelt sich nur um einen Wendepunkt, wenn folgende Kriterien erfüllt sind. | ||
| + | |||
| + | ::<math>\Rightarrow f''(t_0) = 0</math> | ||
| + | ::<math>\Rightarrow f'''(t_0) \neq 0</math> | ||
| + | |||
| − | |||
::{{Lösung versteckt|1= | ::{{Lösung versteckt|1= | ||
| Zeile 22: | Zeile 29: | ||
| − | |||
| + | ::Bei dem Punkt handelt es sich um einen Wendepunkt, da die dritte Ableitung <math>f'''(t) = \frac{3}{2} \Rightarrow f'''( \frac{4}{3}a ) = \frac{3}{2}</math> ungleich Null ist. | ||
| − | |||
| − | ::< | + | ::<u>Der Punkt, an welchem die Funktion besonders stark abfällt ist zugleich der Wendepunkt</u> <math>WP \left( \frac{4}{3}a / \frac{4}{27}a^3 \right)</math> |
| − | + | ||
}} | }} | ||
Version vom 23. Januar 2010, 21:12 Uhr
Bestimmung der größten Senkung der Durchflussgeschwindigkeit
Es soll, in Abhängigkeit von a bestimmt werden, wann die Druchflussgeschwindigkeit besonders stark absinkt. Dieser Wert soll zum Zeitpunkt t berechnet werden.
|
Die blaue Funktion zeigt die Ableitung f '(t) der schwarzen Funktion f (t) für a = 3. |
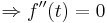
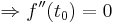
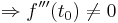
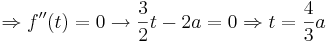
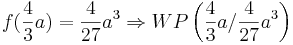
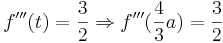 ungleich Null ist.
ungleich Null ist.