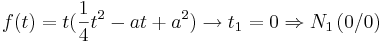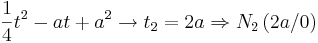Nullstellen: Unterschied zwischen den Versionen
Aus RMG-Wiki
(/Link geändert) |
|||
| Zeile 20: | Zeile 20: | ||
<popup name="Rechnerische Lösung"> | <popup name="Rechnerische Lösung"> | ||
| − | :Durch Ausklammern von t erhält man zum einen die erste Nullstelle, zum anderen auch eine quadratische Funktion, welche man mit Hilfe der [http://de.wikipedia.org/wiki/Quadratische_Gleichung#L.C3.B6sungsformeln | + | :Durch Ausklammern von t erhält man zum einen die erste Nullstelle, zum anderen auch eine quadratische Funktion, welche man mit Hilfe der [http://de.wikipedia.org/wiki/Quadratische_Gleichung#L.C3.B6sungsformeln Lösungsformel für quadratische Gleichungen] lösen kann. |
:<math>f(t) = t (\frac{1}{4} t^2 - a t + a^2) \rightarrow t_1 = 0 \Rightarrow N_1\left( 0 / 0 \right) </math> | :<math>f(t) = t (\frac{1}{4} t^2 - a t + a^2) \rightarrow t_1 = 0 \Rightarrow N_1\left( 0 / 0 \right) </math> | ||
Version vom 23. Januar 2010, 20:08 Uhr
Aufgabe: Nullstellen
Es soll bestimmt werden, abhängig vom Parameter a, zu welchen Monaten kein Wasser durch den Fluss fließt.
|
|