Übungsaufgaben: Unterschied zwischen den Versionen
(→Übungsaufgaben) |
|||
| Zeile 110: | Zeile 110: | ||
| + | <span style="color: blue">Aufgabe 5:</span> <br /> | ||
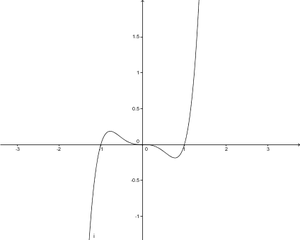
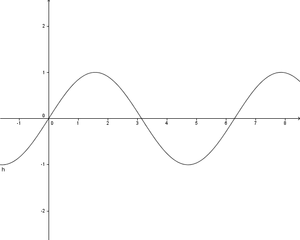
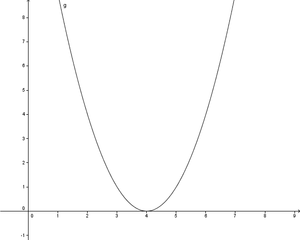
| + | Ordne den abgeblideten Graphen ihren Funktionsterm zu. Alle Funktionen sind aus der unten abgebildeten Funktion f(x)=x<sup>5</sup>-x<sup>3</sup>+1. <br /> <br /> | ||
[[Bild:Übungsaufgabe 6.5.1png|300px]] | [[Bild:Übungsaufgabe 6.5.1png|300px]] | ||
| Zeile 124: | Zeile 126: | ||
</div> | </div> | ||
| − | + | <span style="color: blue">Aufgabe 6: Abschlusstest</span> | |
| + | Der folgende Multiplechoice-Test ist die letzte Aufgabe des Lernpfades. Er deckt alle behandelten Themengebiete ab. Wenn du bei einigen Aufgaben nicht weiter weißt, kannst du deine Notizen zur Rate ziehen. Sollte auch das nicht helfen, solltest du dir die entsprechenden Kapitel noch einmal anschauen und deine Notizen eventuell überarbeiten. Wie immer können mehrere Antwortmöglichkeiten richtig sein. | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | '''Die Funktion f(x)={(3x+3) \over(2x-1)} ist eine''' (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion) | + | '''1.Die Funktion f(x)={(3x+3) \over(2x-1)} ist eine''' (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion) |
| − | '''Eine Funktion, die keinen Grenzwert besitzt, ist''' (Divergent) (!Konvergent.) (!Punktsymmetrisch zum Ursprung) (!Gebrochen rational) | + | '''2. Eine Funktion, die keinen Grenzwert besitzt, ist''' (Divergent) (!Konvergent.) (!Punktsymmetrisch zum Ursprung) (!Gebrochen rational) |
| − | '''Der Zusammenhang g(x)=f(-x) entspricht''' (!Einer Achsensymmetrie zur y-Achse) (!Einer Spiegelung an der x-Achse) (!Einer Punktsymmetrie zum Ursprung) (Einer Spiegelung an der y-Achse) (!Einer Streckung in x-Richtung) | + | '''3. Der Zusammenhang g(x)=f(-x) entspricht''' (!Einer Achsensymmetrie zur y-Achse) (!Einer Spiegelung an der x-Achse) (!Einer Punktsymmetrie zum Ursprung) (Einer Spiegelung an der y-Achse) (!Einer Streckung in x-Richtung) |
| − | '''Der abgebildete Graph der Funktion f(x)=x<sup>4</sup>-3x<sup>2</sup>+1 ist''' (!Punktsymmetrisch zum Ursprung) (Gerade) (Ganzrational) (!Quadratisch) (Achsensymmetrisch zur y-Achse) (!Ungerade) (Divergent) (!Konvergent) | + | '''4. Der abgebildete Graph der Funktion f(x)=x<sup>4</sup>-3x<sup>2</sup>+1 ist''' (!Punktsymmetrisch zum Ursprung) (Gerade) (Ganzrational) (!Quadratisch) (Achsensymmetrisch zur y-Achse) (!Ungerade) (Divergent) (!Konvergent) |
| − | ''' Der Funktionsterm der Funktion g(x), die von f(x)=2x<sup>4</sup>-x<sup>3</sup> ausgehend um den Faktor 3 in y-Richtung getreckt und anschließend um 2 Einheiten nach oben verschoben wird, lautet''' (6x<sup>4</sup>-3x<sup>3</sup>+2) (!2[3x]<sup>4</sup>-[2x]<sup>3</sup>+2) (!6x<sup>4</sup>-3x<sup>3</sup>+6) (!5x<sup>4</sup>-3x<sup>3</sup>+1) (!6[x+2]<sup>4</sup>-3[x+2]<sup>3</sup>) (!6x<sup>4</sup>-3x<sup>3</sup>) | + | ''' 5. Der Funktionsterm der Funktion g(x), die von f(x)=2x<sup>4</sup>-x<sup>3</sup> ausgehend um den Faktor 3 in y-Richtung getreckt und anschließend um 2 Einheiten nach oben verschoben wird, lautet''' (6x<sup>4</sup>-3x<sup>3</sup>+2) (!2[3x]<sup>4</sup>-[2x]<sup>3</sup>+2) (!6x<sup>4</sup>-3x<sup>3</sup>+6) (!5x<sup>4</sup>-3x<sup>3</sup>+1) (!6[x+2]<sup>4</sup>-3[x+2]<sup>3</sup>) (!6x<sup>4</sup>-3x<sup>3</sup>) |
| − | ''' <math>\lim_{x\to\infty} {2x+1 \over 0,5x+2}=</math>''' (!Unendlich) (!2) (!1) (!0) (4) (!-2) (0,5) | + | '''6. <math>\lim_{x\to\infty} {2x+1 \over 0,5x+2}=</math>''' (!Unendlich) (!2) (!1) (!0) (4) (!-2) (0,5) |
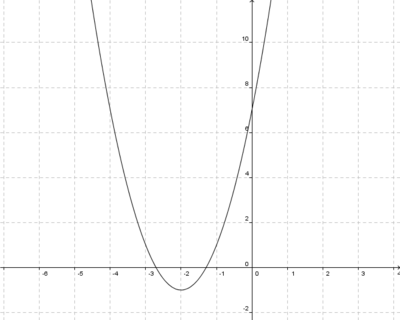
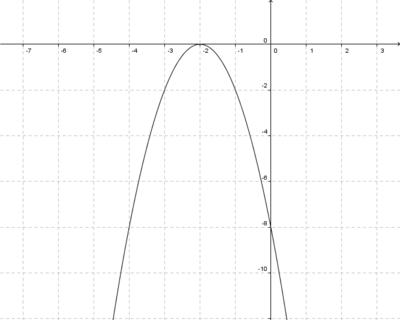
| − | ''' Der Graph der Funktion f(x)=2x<sup>2</sup>+1 ist gegenüber dem Graphen g(x)=x<sup>2</sup>-1 ''' (!In y-Richtung Gestreckt und nach unten verschoben) (Nach oben verschoben ) (In y-Richtung gestreckt und in positiver y-Richtung verschoben ) (In y-Richtung gestreckt ) (!In negativer y-Richtung verschoben) (!Gar nicht verschoben) (!Gar nicht gestreckt) | + | '''7. Der Graph der Funktion f(x)=2x<sup>2</sup>+1 ist gegenüber dem Graphen g(x)=x<sup>2</sup>-1 ''' (!In y-Richtung Gestreckt und nach unten verschoben) (Nach oben verschoben ) (In y-Richtung gestreckt und in positiver y-Richtung verschoben ) (In y-Richtung gestreckt ) (!In negativer y-Richtung verschoben) (!Gar nicht verschoben) (!Gar nicht gestreckt) |
| − | ''' Was trifft auf diese Funktion zu? f(x)=sinx''' (Punktsymmetrie zum Ursprung) (Trigonometrisch) (!Linear) (!Graph: Parabel) (!Keine Nullstellen) (Ungerade) (!Achsensymmetrie zur y-Achse) (!f[0]=0) | + | '''8. Was trifft auf diese Funktion zu? f(x)=sinx''' (Punktsymmetrie zum Ursprung) (Trigonometrisch) (!Linear) (!Graph: Parabel) (!Keine Nullstellen) (Ungerade) (!Achsensymmetrie zur y-Achse) (!f[0]=0) |
| − | ''' Bei einer Streckung in x-Richtung ''' (!Verändert sich die Amplitude einer trigonometrischen Funktion) (Bleiben die Funktionswerte an der Stelle x=0 unverändert ) (!Bleiben die Nullstellen unverändert) (!Wird der Graph an der x-Achse gespiegelt) (Erfolgt die Streckung um den Faktor {1 \over k}) | + | '''9. Bei einer Streckung in x-Richtung ''' (!Verändert sich die Amplitude einer trigonometrischen Funktion) (Bleiben die Funktionswerte an der Stelle x=0 unverändert ) (!Bleiben die Nullstellen unverändert) (!Wird der Graph an der x-Achse gespiegelt) (Erfolgt die Streckung um den Faktor {1 \over k}) |
| − | ''' Um einen Graphen an der y-Achse zu spiegeln''' (!Multipliziert man den Funktionsterm mit -1) (Setzt man für f[x] f[x]ein ) (Schreibt man vor jedes x ein „Minus“ ) (!Verschiebt man den Graphen nach rechts oder links [je nach Lage]) | + | '''10. Um einen Graphen an der y-Achse zu spiegeln''' (!Multipliziert man den Funktionsterm mit -1) (Setzt man für f[x] f[x]ein ) (Schreibt man vor jedes x ein „Minus“ ) (!Verschiebt man den Graphen nach rechts oder links [je nach Lage]) |
| − | ''' Um was für eine Funktion handelt es sich? ''' (Exponentialfunktion) (!ineare Funktion ) (!Trigonometrische Funktion) (!Gebrochen rationale Funktion) | + | '''11. Um was für eine Funktion handelt es sich? ''' (Exponentialfunktion) (!ineare Funktion ) (!Trigonometrische Funktion) (!Gebrochen rationale Funktion) |
| − | ''' <math>\lim_{x\to\infty} {sinx \over x}=</math>''' (!Existiert nicht) (!Unendlich) (0)(!1) | + | '''12. <math>\lim_{x\to\infty} {sinx \over x}=</math>''' (!Existiert nicht) (!Unendlich) (0)(!1) |
| − | '''Wie lautet der Funktionsterm der Funktion g(x), die von f(x)=x<sup>3</sup>x<sup>2</sup>-1 ausgehend zwei Einheiten weiter rechts verläuft?''' (![x+2]<sup>3</sup>+[x+2]<sup>2</sup>-1) (!x<sup>3</sup>+x<sup>2</sup>+1) ([x-2]<sup>3</sup>+[x-2]<sup>2</sup>-1) (!x<sup>3</sup>+x<sup>2</sup>-3) (x<sup>3</sup>-5x<sup>2</sup>+8x-5) (!x<sup>3</sup>+5x<sup>2</sup>-8x+5) | + | '''13. Wie lautet der Funktionsterm der Funktion g(x), die von f(x)=x<sup>3</sup>x<sup>2</sup>-1 ausgehend zwei Einheiten weiter rechts verläuft?''' (![x+2]<sup>3</sup>+[x+2]<sup>2</sup>-1) (!x<sup>3</sup>+x<sup>2</sup>+1) ([x-2]<sup>3</sup>+[x-2]<sup>2</sup>-1) (!x<sup>3</sup>+x<sup>2</sup>-3) (x<sup>3</sup>-5x<sup>2</sup>+8x-5) (!x<sup>3</sup>+5x<sup>2</sup>-8x+5) |
Version vom 20. Januar 2010, 21:32 Uhr
Übungsaufgaben Aufgabe 1:
Aufgabe 4:
Aufgabe 6: Abschlusstest Der folgende Multiplechoice-Test ist die letzte Aufgabe des Lernpfades. Er deckt alle behandelten Themengebiete ab. Wenn du bei einigen Aufgaben nicht weiter weißt, kannst du deine Notizen zur Rate ziehen. Sollte auch das nicht helfen, solltest du dir die entsprechenden Kapitel noch einmal anschauen und deine Notizen eventuell überarbeiten. Wie immer können mehrere Antwortmöglichkeiten richtig sein. 1.Die Funktion f(x)={(3x+3) \over(2x-1)} ist eine (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion) 2. Eine Funktion, die keinen Grenzwert besitzt, ist (Divergent) (!Konvergent.) (!Punktsymmetrisch zum Ursprung) (!Gebrochen rational) 3. Der Zusammenhang g(x)=f(-x) entspricht (!Einer Achsensymmetrie zur y-Achse) (!Einer Spiegelung an der x-Achse) (!Einer Punktsymmetrie zum Ursprung) (Einer Spiegelung an der y-Achse) (!Einer Streckung in x-Richtung) 4. Der abgebildete Graph der Funktion f(x)=x4-3x2+1 ist (!Punktsymmetrisch zum Ursprung) (Gerade) (Ganzrational) (!Quadratisch) (Achsensymmetrisch zur y-Achse) (!Ungerade) (Divergent) (!Konvergent) 5. Der Funktionsterm der Funktion g(x), die von f(x)=2x4-x3 ausgehend um den Faktor 3 in y-Richtung getreckt und anschließend um 2 Einheiten nach oben verschoben wird, lautet (6x4-3x3+2) (!2[3x]4-[2x]3+2) (!6x4-3x3+6) (!5x4-3x3+1) (!6[x+2]4-3[x+2]3) (!6x4-3x3) 6. 7. Der Graph der Funktion f(x)=2x2+1 ist gegenüber dem Graphen g(x)=x2-1 (!In y-Richtung Gestreckt und nach unten verschoben) (Nach oben verschoben ) (In y-Richtung gestreckt und in positiver y-Richtung verschoben ) (In y-Richtung gestreckt ) (!In negativer y-Richtung verschoben) (!Gar nicht verschoben) (!Gar nicht gestreckt) 8. Was trifft auf diese Funktion zu? f(x)=sinx (Punktsymmetrie zum Ursprung) (Trigonometrisch) (!Linear) (!Graph: Parabel) (!Keine Nullstellen) (Ungerade) (!Achsensymmetrie zur y-Achse) (!f[0]=0) 9. Bei einer Streckung in x-Richtung (!Verändert sich die Amplitude einer trigonometrischen Funktion) (Bleiben die Funktionswerte an der Stelle x=0 unverändert ) (!Bleiben die Nullstellen unverändert) (!Wird der Graph an der x-Achse gespiegelt) (Erfolgt die Streckung um den Faktor {1 \over k}) 10. Um einen Graphen an der y-Achse zu spiegeln (!Multipliziert man den Funktionsterm mit -1) (Setzt man für f[x] f[x]ein ) (Schreibt man vor jedes x ein „Minus“ ) (!Verschiebt man den Graphen nach rechts oder links [je nach Lage]) 11. Um was für eine Funktion handelt es sich? (Exponentialfunktion) (!ineare Funktion ) (!Trigonometrische Funktion) (!Gebrochen rationale Funktion) 12. 13. Wie lautet der Funktionsterm der Funktion g(x), die von f(x)=x3x2-1 ausgehend zwei Einheiten weiter rechts verläuft? (![x+2]3+[x+2]2-1) (!x3+x2+1) ([x-2]3+[x-2]2-1) (!x3+x2-3) (x3-5x2+8x-5) (!x3+5x2-8x+5)
Du hast es geschafft! |
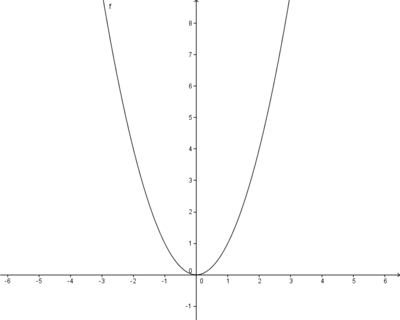
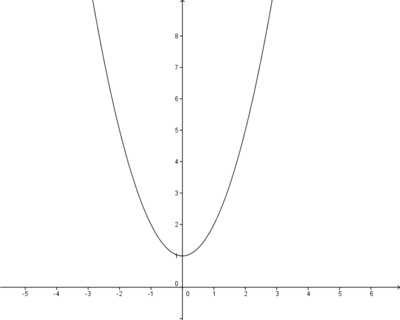
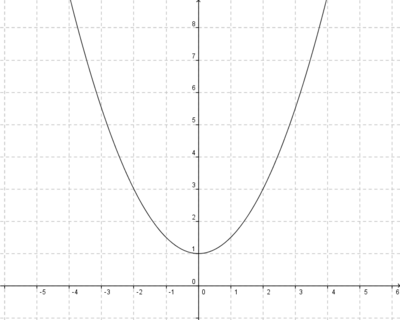
Streckung um 0,5 in y-Richtung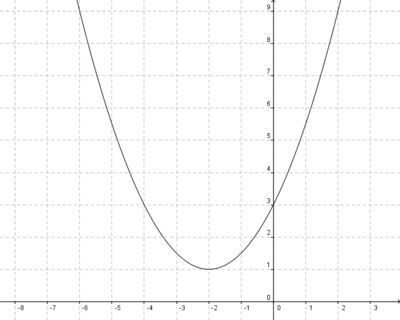 
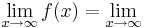4x6+8x5-12x4-24x3=
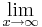4x3(x3+2x2-3x-6)=
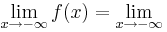4x6+8x5-12x4-24x3=
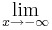4x3(x3+2x2-3x-6)=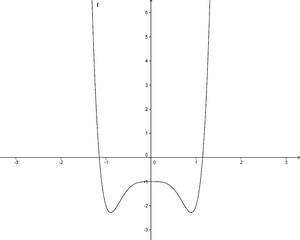
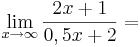(!Unendlich) (!2) (!1) (!0) (4) (!-2) (0,5)
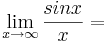(!Existiert nicht) (!Unendlich) (0)(!1)
