Übungsaufgaben: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Übungsaufgaben) |
|||
| Zeile 122: | Zeile 122: | ||
|} | |} | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | '''Die Funktion f(x)={(3x+3) \over(2x-1)} ist eine''' (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion) | ||
| + | |||
| + | '''Eine Funktion, die keinen Grenzwert besitzt, ist''' (Divergent) (!Konvergent.) (!Punktsymmetrisch zum Ursprung) (!Gebrochen rational) | ||
| + | |||
| + | '''Der Zusammenhang g(x)=f(-x) entspricht''' (!Einer Achsensymmetrie zur y-Achse) (!Einer Spiegelung an der x-Achse) (!Einer Punktsymmetrie zum Ursprung) (Einer Spiegelung an der y-Achse) (!Einer Streckung in x-Richtung) | ||
| + | |||
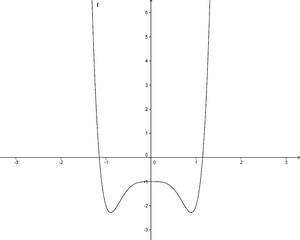
| + | '''Der abgebildete Graph der Funktion f(x)=x<sup>4</sup>-3x<sup>2</sup>+1 ist''' (!Punktsymmetrisch zum Ursprung) (Gerade) (Ganzrational) (!Quadratisch) (Achsensymmetrisch zur y-Achse) (!Ungerade) (Divergent) (!Konvergent) | ||
</div> | </div> | ||
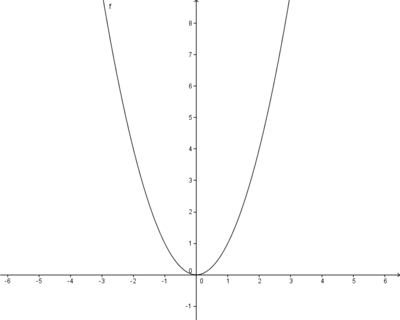
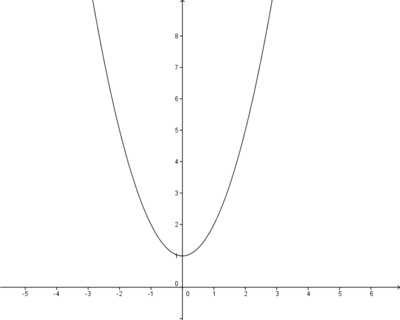
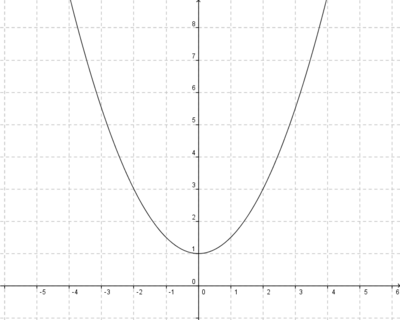
 Streckung um 0,5 in y-Richtung
Streckung um 0,5 in y-Richtung 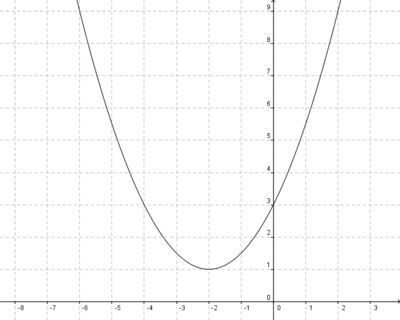
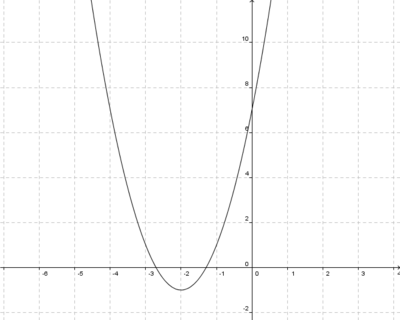
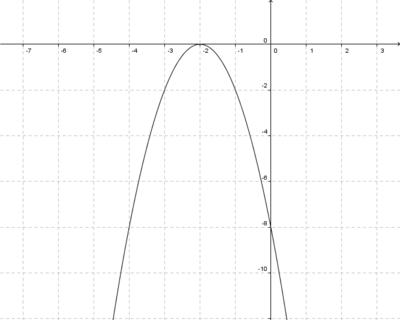
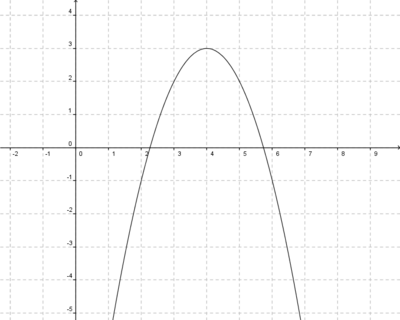

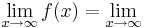 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=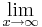 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=
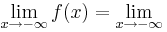 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=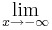 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=