Strecken und Spiegeln von Funktionsgraphen: Unterschied zwischen den Versionen
(→Streckung in y-Richtung) |
(→Streckung in y-Richtung) |
||
| Zeile 4: | Zeile 4: | ||
{| | {| | ||
| − | ! width=" | + | ! width="910" | |
|- | |- | ||
| valign="top" | | | valign="top" | | ||
''' <span style="color: blue">Zur Erinnerung:</span>''' <br /> | ''' <span style="color: blue">Zur Erinnerung:</span>''' <br /> | ||
| − | Bei quadratischen Funktionen haben wir bereits festgestellt, dass der Funktionsgraph durch einen Koeffizienten a weiter oder enger als die Normalparabel f(x)=x<sup>2</sup> sein kann. Diese Erscheinung wird nun allgemein für alle Funktionstypen untersucht. | + | Bei quadratischen Funktionen haben wir bereits festgestellt, dass der Funktionsgraph durch einen Koeffizienten a weiter oder enger als die Normalparabel <br /> |
| + | f(x)=x<sup>2</sup> sein kann. Diese Erscheinung wird nun allgemein für alle Funktionstypen untersucht. | ||
|} | |} | ||
{| | {| | ||
| − | ! width=" | + | ! width="910" | |
|- | |- | ||
| valign="top" | | | valign="top" | | ||
| Zeile 19: | Zeile 20: | ||
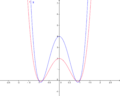
Im untenstehenden Koordinatensystem ist der Graph der Funktion f(x)= 2x<sup>4</sup>-3x<sup>2</sup>+0,5 dargestellt. Wird diese Funktion nun mit einer rationalen Zahl k multipliziert, entsteht ein veränderter Graph g(x). Versuche, durch Verschieben des Reglers das Verhalten des Funktionsgraphen zu erklären. | Im untenstehenden Koordinatensystem ist der Graph der Funktion f(x)= 2x<sup>4</sup>-3x<sup>2</sup>+0,5 dargestellt. Wird diese Funktion nun mit einer rationalen Zahl k multipliziert, entsteht ein veränderter Graph g(x). Versuche, durch Verschieben des Reglers das Verhalten des Funktionsgraphen zu erklären. | ||
|} <br /> <br /> | |} <br /> <br /> | ||
| − | <ggb_applet width="892" height="512" version="3.2" ggbBase64="UEsDBBQACAAIAGqNMjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1stVbBjts2ED0nX0HwlKSILcnr7AaQNmhTBAiwbQ9uUyCHAJQ0llhTpEBSXjlf3xlSsr1uA2yb5ERyOBq+efNm7PzN2Cm2B+uk0QVPFwlnoCtTS90UfPDblzf8ze3TvAHTQGkF2xrbCV/w1SLjZB/k7dMnuWvNPRMquHyQcF9wbwfgzPUWRO1aAB/NW6Ec2sUwSiWFPfxW/gWVd6eLGOO97gc/B6m6+k66+bgM7/VK+p/lXtZgmTJVwV+tETnuPoD1shKq4FdJtGQFzy4u0bSi29ZY+dloT+6n4Fu0MObkZ0BCMrLly5BnDkOlZC2FpmQCDnRi7F7WvkUIq1cYEmTTItZ1msRolTG23hych46NH8EafDtNiOfDdFqHk0Nc9GC6WtzcXF9fp+ssWadXN2t0nO6CYwgK+w14jzVyTIzgZqYaK+vz/Xv3k1H1kdzeSO3fit4PNpR3NZk2/kDhEYQl8D/qRsFkS5H+FqpdacZNJGQVQ/9+6MMnAU7ZvDXKWGaJagTcTGsZ1+BDOI9eSfBJgscUg4Ie79PXWfAIaxnX4KWkjtCmvNM56ZluMUrHyECUoipnOpQoAavM2aClv5sPqIbdKVPy/3XoSuyGcz0cQ6bfKGS+vBBSvgOrQUW5aKzrYAbH9iTLWLqAo4ZKdniMFxMhgor1BwKI1hoaCzPu2EuRrnD7QJIX5nw5gyAMDrFWHmcC5uMpl423KAPQbI+2d4Pe0aVrrOhb0NTQHpup4O+wgJgW+1OqHWe18PgpzQkYcRI4GjKRNoaZ4aQZe1yfjc9ZwbJFwl6w8dOzq0XynL1kq/mc0fkHliyCkHJQ0AE2qA8C3A46wDxWY8sfysS3WA+NTxNj00cTDWFomTCALkp6qj1ef0G0OKr6VuBu7kklDjiMznkO0X4x9UP2hcYqBmpxJvQUgHTSA0SFzRBZjwFDm55J4BF5obgiQ//gSg8dWFkds9wFqhDaMAFcLb4xM+kjmZn8nArzvJM60so6MVJn01aUzqjBw6ZCfes7UwUKZ3TTBE6T4DvS+M3CiKWpTJutHOE0CP997j9KNP+/eg8Kc9EOBW+mbmhiN+xQ+9QYnD1C88330/w8zr9a9f9RucvzGRR+gKc/ILd/A1BLBwj4av0LTAMAALIIAABQSwECFAAUAAgACABqjTI8+Gr9C0wDAACyCAAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAIYDAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | + | <ggb_applet width="892" height="512" version="3.2" ggbBase64="UEsDBBQACAAIAGqNMjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1stVbBjts2ED0nX0HwlKSILcnr7AaQNmhTBAiwbQ9uUyCHAJQ0llhTpEBSXjlf3xlSsr1uA2yb5ERyOBq+efNm7PzN2Cm2B+uk0QVPFwlnoCtTS90UfPDblzf8ze3TvAHTQGkF2xrbCV/w1SLjZB/k7dMnuWvNPRMquHyQcF9wbwfgzPUWRO1aAB/NW6Ec2sUwSiWFPfxW/gWVd6eLGOO97gc/B6m6+k66+bgM7/VK+p/lXtZgmTJVwV+tETnuPoD1shKq4FdJtGQFzy4u0bSi29ZY+dloT+6n4Fu0MObkZ0BCMrLly5BnDkOlZC2FpmQCDnRi7F7WvkUIq1cYEmTTItZ1msRolTG23hych46NH8EafDtNiOfDdFqHk0Nc9GC6WtzcXF9fp+ssWadXN2t0nO6CYwgK+w14jzVyTIzgZqYaK+vz/Xv3k1H1kdzeSO3fit4PNpR3NZk2/kDhEYQl8D/qRsFkS5H+FqpdacZNJGQVQ/9+6MMnAU7ZvDXKWGaJagTcTGsZ1+BDOI9eSfBJgscUg4Ie79PXWfAIaxnX4KWkjtCmvNM56ZluMUrHyECUoipnOpQoAavM2aClv5sPqIbdKVPy/3XoSuyGcz0cQ6bfKGS+vBBSvgOrQUW5aKzrYAbH9iTLWLqAo4ZKdniMFxMhgor1BwKI1hoaCzPu2EuRrnD7QJIX5nw5gyAMDrFWHmcC5uMpl423KAPQbI+2d4Pe0aVrrOhb0NTQHpup4O+wgJgW+1OqHWe18PgpzQkYcRI4GjKRNoaZ4aQZe1yfjc9ZwbJFwl6w8dOzq0XynL1kq/mc0fkHliyCkHJQ0AE2qA8C3A46wDxWY8sfysS3WA+NTxNj00cTDWFomTCALkp6qj1ef0G0OKr6VuBu7kklDjiMznkO0X4x9UP2hcYqBmpxJvQUgHTSA0SFzRBZjwFDm55J4BF5obgiQ//gSg8dWFkds9wFqhDaMAFcLb4xM+kjmZn8nArzvJM60so6MVJn01aUzqjBw6ZCfes7UwUKZ3TTBE6T4DvS+M3CiKWpTJutHOE0CP997j9KNP+/eg8Kc9EOBW+mbmhiN+xQ+9QYnD1C88330/w8zr9a9f9RucvzGRR+gKc/ILd/A1BLBwj4av0LTAMAALIIAABQSwECFAAUAAgACABqjTI8+Gr9C0wDAACyCAAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAIYDAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> <br /> <br /> |
| + | {| | ||
| + | ! width="910" | | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | ''' <span style="color: blue">Erklärung:</span>''' <br /> | ||
| + | Da der Graph von g(x) aus einer Multiplikation von einem Koeffizienten k und dem Funktionswert von f(x) entsteht, gilt für den Graphen g die Funktionsgleichung g(x)=k×f(x). Dadurch nimmt g bei einem Koeffizienten k>1 einen größeren Funktionswert an als der Graph von f. Der Graph ist also in y-Richtung gestreckt. Dasselbe gilt auch für 0<k<1, nur das der Graph g hier kleinere Funktionswerte annimmt. '''Die Nullstellen bleiben dabei unverändert!''' | ||
| + | |} <br /> <br /> <br /> | ||
| − | + | {| | |
| − | + | ! width="950" | | |
| + | |- | ||
| + | | valign="top" | | ||
<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> ''' <span style="color: blue">Beispiel:</span>''' <br /> | <div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> ''' <span style="color: blue">Beispiel:</span>''' <br /> | ||
:<span style="color: green">k=3</span> <br /> | :<span style="color: green">k=3</span> <br /> | ||
| Zeile 30: | Zeile 40: | ||
::g(1)=<span style="color: red">f(1)</span><span style="color: green"><math>\times</math>3</span> <br /> | ::g(1)=<span style="color: red">f(1)</span><span style="color: green"><math>\times</math>3</span> <br /> | ||
::g(1)=-0,5<math>\times</math>3 <br /> | ::g(1)=-0,5<math>\times</math>3 <br /> | ||
| − | ::g(1)=-1,5 </div> <br /> <br /> <br /> <br /> | + | ::g(1)=-1,5 </div> |
| + | |} <br /> <br /> <br /> <br /> | ||
== <span style="color: blue">Streckung in x-Richtung</span> == | == <span style="color: blue">Streckung in x-Richtung</span> == | ||
Version vom 18. Januar 2010, 19:34 Uhr
Inhaltsverzeichnis |
Strecken und Spiegeln von Funktionsgraphen
Streckung in y-Richtung
|
Zur Erinnerung: |
|
Problemstellung: |
|
Erklärung: |
|
Beispiel:
|
Streckung in x-Richtung
Problemstellung:
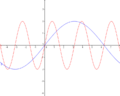
Im nebenstehenden Koordinatensystem ist der Graph der Funktion f(x)=cosx eingezeichnet. Durch eine Streckung in x-Richtung um den Faktor 3 entsteht der Graph g. Wie lautet der Funktionsterm von g?
Erklärung: Eine Streckung um den Faktor 3 in x-Richtung bedeutet, dass der Graph von g den Funktionswert, den der Graph von f an der Stelle x annimmt, erst an der Stelle 3x annimmt.
Es entsteht also der Zusammenhang f(x)=g(3x) oder g(x)=f(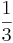 x)=cos
x)=cos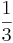 x
x
(Allgemein: f(x)=g(kx) oder g(x)=f(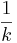 x))
x))
- k=2
- f(
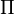 )=-1
)=-1
- g(x)=f(
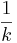 x)
x)
- g(
 )=f(
)=f(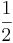
 )
)
- g(
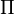 )=0
)=0
- g(x)=f(
Ist der Streckungsfaktor 0<k<1, z.B. k=0,5, dann entspricht der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle 0,5.
Der Zusammenhang lautet also f(x)=g(0,5x) oder g(x)=f(2x). Das Verhalten des Graphen kannst du beobachten, wenn du im oben abgebildeten Koordinatensystem den Regler k verschiebst.
Der Funktionswert an der Stelle x=0 bleibt immer gleich.
Allgemein: g(x)=f(kx) mit dem Streckungsfaktor 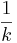
Besteht zwischen zwei Funktionen der Zusammenhang g(x)=k×f(x) mit k>0, dann ist der Graph von g gegenüber dem von f in y-Richtung um den Faktor k gestreckt.
Besteht zwischen zwei Funktionen der Zusammenhang g(x)=f(kx) mit k>0, dann ist der Graph von g gegenüber dem von f um den Faktor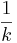 in x-Richtung gestreckt.
in x-Richtung gestreckt.Spiegelung an der x-Achse
Bisher haben wir das Verhalten der Funktionsgraphen nur für positive Werte von k untersucht. Nun soll k den Wert -1 annehmen. Aus den oben erstellten Formeln ergeben sich nun die Fälle
g(x)= -1k×f(x) und g(x)=f(-1kx), also g(x)= -f(x) und g(x)=f(-x).
Zunächst betrachten wir den Fall g(x)= -f(x).
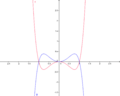
Im nebenstehenden Koordinatensystem ist der Graph von f mit dem Funktionsterm f(x)=x4-x2 rot dargestellt. Um die Funktionswerte des grün dargestellten Graphen von g zu erhalten, werden die Funktionswerte von f(x) mit k=-1 multipliziert. Wie in der Abbildung zu erkennen ist, handelt es sich beim Graphen von g um eine Spiegelung an der x-Achse.
Spiegelung an der y-Achse
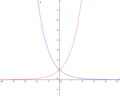
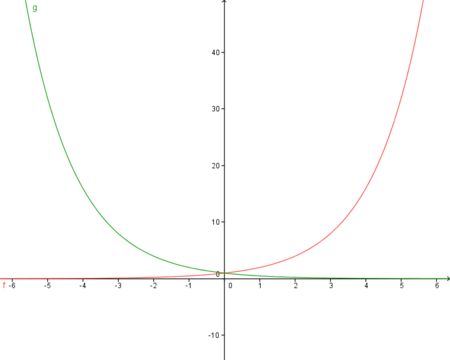
Nun betrachten wir den Fall g(x)=f(-x) am Beispiel f(x)=2x.
Im nebenstehenden Koordinatensystem ist der Graph von f rot dargestellt. Für den Graphen von g (grün dargestellt) gilt der Funktionsterm g(x)=2-x. Betrachtet man die beiden Graphen zusammen, so fällt auf, dass der Graph von g aus einer Spiegelung von f an der y-Achse entsteht.
Der Graph von g mit g(x)= -f(x) geht aus dem Graphen von f durch eine Spiegelung an der x-Achse hervor.
Der Graph von g mit g(x)=f(-x) geht aus dem Graphen von f durch eine Spiegelung an der y-Achse hervor.
Beispielaufgaben
Aufgabe 1:
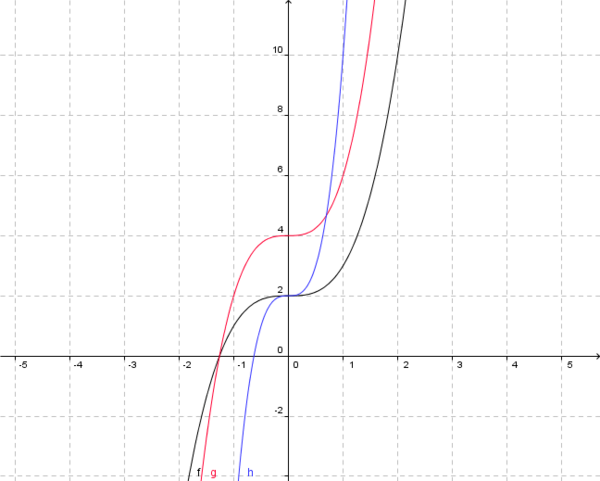
Zeichne in ein gemeinsames Koordinatensystem die Funktion f(x)=x3+2, sowie die Funktionen g(x)=2f(x) und h(x)=f(2x).
Aufgabe 2:
Gegeben ist die Funktion f(x)=2x3-x2+2x+1. Erstelle jeweils die neuen Funktionen nach den folgenden Anweisungen. Verwende zum Weiterrechnen jeweils den vorangegangenen Funktionsterm.
- a) Streckung um den Faktor 3 in y-Richtung
- b) Spiegelung an der x-Achse
- c) Streckung um den Faktor 0,5 in x-Richtung
- d) Streckung um den Faktor 0,25 in y-Richtung
- e) Spiegelung an der y-Achse
Aufgabe 3:
Finde die passenden Paare.
 k
k 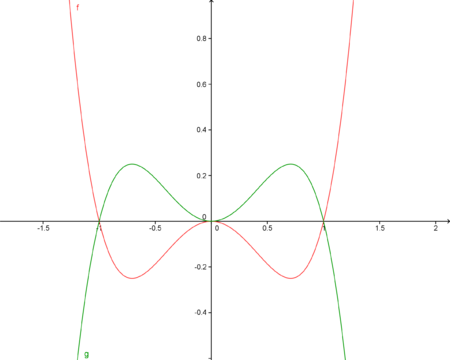
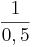 =2
=2