Lösung von Teilaufgabe c: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
Zeile 78: Zeile 78:
 
     0 = ( x<sub>0</sub><sup>2</sup> - 2x<sub>0</sub> - 2 ) ( e<sup>4 - x<sub>0</sub></sup> )                            | e<sup>4 - x<sub>0</sub></sup> > 0
 
     0 = ( x<sub>0</sub><sup>2</sup> - 2x<sub>0</sub> - 2 ) ( e<sup>4 - x<sub>0</sub></sup> )                            | e<sup>4 - x<sub>0</sub></sup> > 0
 
  --> 0 = ( x<sub>0</sub><sup>2</sup> - 2x<sub>0</sub> - 2 )
 
  --> 0 = ( x<sub>0</sub><sup>2</sup> - 2x<sub>0</sub> - 2 )
 +
 +
Lösen quadratischer Gleichungen mit Hilfe der Mitternachtsformel
 +
[http://de.wikipedia.org/wiki/Mitternachtsformel?title=Mitternachtsformel&redirect=no Mitternachtsformel]
 +
 +
<math> x_{1,2} = \frac{2\pm\sqrt{4--8}}{2}</math><br />
 +
<math> x_{1,2} = \frac{2\pm\sqrt{4+8}}{2}</math><br />
 +
<math> x_{1,2} = \frac{2\pm\sqrt{12}}{2}</math><br />
 +
<math> x_{1,2} = \frac{2\pm\sqrt{4\cdot 3}}{2}</math><br />
 +
<math> x_{1,2} = \frac{2\pm2\cdot\sqrt{3}}{2}</math><br />
 +
<math> x_{1,2} = {1\pm\sqrt{3}}</math>
 +
 +
<math> x_{1} = {1\p\sqrt{3}}</math><br />
 +
<math> x_{2} = {1\m\sqrt{3}}</math>

Version vom 4. Januar 2010, 18:30 Uhr

Inhaltsverzeichnis

Tangente im Punkt Wa ( a + 2 / 2 ) an Gfa mit dem Schnittpunkt A (0 / 2012 )

Lösung; Tangentengleichung

Allgemeine Tangentengleichung: siehe Formelsammlung Seite ......

y = f'( x0 ) ( x - x0 ) + f ( x0 )


mit:
x = 0
y = 2012
x0 = a + 2
fa( x0 ) = fa( a + 2 ) = 2
f'a( x0 ) = f'a( a + 2 ) = m = -1

          f'( a + 2 ) = ea + 2 - ( a + 2 )  ( 1 + a - ( a + 2 ) )
                      = ea + 2 - a - 2 )  ( 1 + a - a - 2 ) )
                      = e 0 ( -1 )
                      = -1

    y = f'( a + 2 ) ( x - ( a + 2 )) + f ( a + 2 )
    y = (-1) ( x - a - 2 ) + 2
    y = -x + a + 2 + 2 
    y = -x + a + 4 
 2012 = 0 + a + 4          / -4
    a = 2008

Lösung; Fußweg 

              y = m x + t   
       fa( x0 ) = f'a( x0 ) x0 + t     
    fa( a + 2 ) = f'a( a + 2 ) x0 + t
              2 = -1 x0 + t       / - ( -1 x0 )
              t = 2 - ( -1 x0 )
              t = 2 - ( -1 ( a + 2 ))
              t = 2 - ( -a - 2)
              t = 2 + a + 2 
              t = a + 4          |einsetzen in y = m x + t 

    y = m x + a + 4
 2012 = -1*0 + a + 4
 2012 = a + 4 
    a = 2008

Lösung; Clever 

\frac{y2 - y1}{x2 - x1} = f'a ( x )

\frac{2012 - 2}{0 - ( a + 2 )} = -1

\frac{2010}{(-a - 2 )} = -1          | *( -a - 2 )

2010 = a + 2
2008 = a


Berechnung derjenigen Punkte, für welche die Tangente an den Graphen von f2 durch den Ursprung verläuft

Verwendung der Tangentialgleichung 

y = f'( x0 ) ( x - x0 ) + f ( x0 )


y = ( x0 - a - 1 ) ( -ea + 2 - x0 ) ( x - x0 ) + ( x0 - a ) ea + 2 - x0

mit:

y = 0

x = 0

a = 2


    0 = ( x0 - 3 ) ( -e4 - x0 ) ( -x0 ) + ( x0 - 2 ) ( e4 - x0 )
    0 = ( x0 - 3 ) ( e4 - x0 ) ( x0 ) + ( x0 - 2 ) ( e4 - x0 )
    0 = ( x02 - 3x0 ) ( e4 - x0 ) + ( x0 - 2 ) ( e4 - x0 )
    0 = ( x02 - 3x0 + x0 - 2 ) ( e4 - x0 )
    0 = ( x02 - 2x0 - 2 ) ( e4 - x0 )                             | e4 - x0 > 0
--> 0 = ( x02 - 2x0 - 2 )

Lösen quadratischer Gleichungen mit Hilfe der Mitternachtsformel Mitternachtsformel

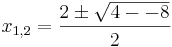
x_{1,2} = \frac{2\pm\sqrt{4--8}}{2}
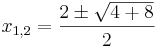
x_{1,2} = \frac{2\pm\sqrt{4+8}}{2}
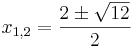
x_{1,2} = \frac{2\pm\sqrt{12}}{2}
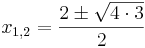
x_{1,2} = \frac{2\pm\sqrt{4\cdot 3}}{2}
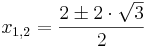
x_{1,2} = \frac{2\pm2\cdot\sqrt{3}}{2}
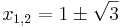
x_{1,2} = {1\pm\sqrt{3}}

Fehler beim Parsen(Unbekannte Funktion „\p“): x_{1} = {1\p\sqrt{3}}
Fehler beim Parsen(Unbekannte Funktion „\m“): x_{2} = {1\m\sqrt{3}}

Von „http://rmg.zum.de/index.php?title=Facharbeit_Andre_Etzel/Teilaufgabe_c/Lösung_von_Teilaufgabe_c&oldid=25673“