Teilaufgabe a: Unterschied zwischen den Versionen

Version vom 31. Dezember 2009, 00:47 Uhr

Für jede reelle Zahl a sei eine Funktion f_a durch y = f_a (x) = ( x - a ) e^{a + 2 - x} mit 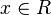$x\in R$ gegeben.

1.Untersuchen Sie den Graphen von f_a auf:

Bestimmen Sie gegebenenfalls deren Koordinaten!

2.Alle Extrempunkte liegen auf dem Graphen einer Funktion h. Geben Sie eine Funktionsgleichung von h an!

3.Skizzieren Sie den Graphen der Funktion f₂ für 1,6 < x <7!

@@ Zeile 1: / Zeile 1: @@
-Für jede reelle Zahl a sei eine Funktion '''f<sub>a</sub>''' durch '''y=f<sub>a</sub>(x)=(x-a)e<sup>a+2-x</sup>''' mit xeR gegeben.
+Für jede reelle Zahl a sei eine Funktion '''f<sub>a</sub>''' durch '''y = f<sub>a</sub> (x) = ( x - a ) e<sup>a + 2 - x</sup>''' mit <math>x\in R</math> gegeben.
-:a) 1.Untersuchen Sie den Graphen von '''f<sub>a</sub>''' auf:
+:1.Untersuchen Sie den Graphen von '''f<sub>a</sub>''' auf:
 ::*Schnittpunkte mit den Koordinatenachsen,
 ::*lokale Extrempunkte und
 ::*Wendepunkte!
 ::Bestimmen Sie gegebenenfalls deren Koordinaten!
 :2.Alle Extrempunkte liegen auf dem Graphen einer Funktion h. Geben Sie eine Funktionsgleichung von h an!
 :3.Skizzieren Sie den Graphen der Funktion '''f<sub>2</sub>''' für '''1,6 <u><</u> x <u><</u>7!'''
 [[Lösung zur Teilaufgabe a)]]