Einführung: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
Um euch das Thema etwas näher zu bringen, wollen wir einen linearen Zusammenhang zunächst an einem Beispiel veranschaulichen, auf das wir im Laufe des Lernpfades gelegentlich zurückkommen werden.<br /><br /> | Um euch das Thema etwas näher zu bringen, wollen wir einen linearen Zusammenhang zunächst an einem Beispiel veranschaulichen, auf das wir im Laufe des Lernpfades gelegentlich zurückkommen werden.<br /><br /> | ||
| − | Noch einmal kurz zur Wiederholung: '''Proportionale Zuordnungen''' solltet ihr im Unterricht bereits besprochen haben. Eine solche Zuordnung liegt dann vor, wenn sich zwei Größen zueinander proportional verhalten. Das heißt sie steigen bzw. fallen im gleichen Verhältnis und haben somit immer einen konstanten Quotienten q=2. Größe / 1. Größe. (verdoppelt sich z.B. der Wert der x-Koordinate, so verdopplet sich auch der Wert der y-Koordinate)<br />Dies nennt man dann auch einen '''linearen Zusammenhang''', den man mit einer linearen Funktion beschreiben kann. Ihr Graf ist eine '''Gerade'''. | + | {| class="prettytable" |
| + | |- | ||
| + | | 1 |Noch einmal kurz zur Wiederholung: | ||
| + | '''Proportionale Zuordnungen''' solltet ihr im Unterricht bereits besprochen haben. Eine solche Zuordnung liegt dann vor, wenn sich zwei Größen zueinander proportional verhalten. Das heißt sie steigen bzw. fallen im gleichen Verhältnis und haben somit immer einen konstanten Quotienten q=2. Größe / 1. Größe. (verdoppelt sich z.B. der Wert der x-Koordinate, so verdopplet sich auch der Wert der y-Koordinate)<br />Dies nennt man dann auch einen '''linearen Zusammenhang''', den man mit einer linearen Funktion beschreiben kann. Ihr Graf ist eine '''Gerade'''. | ||
| + | |||
| + | |- | ||
| + | |||
| + | |}<br /> | ||
Nun zum Beispiel:<br /> | Nun zum Beispiel:<br /> | ||
| Zeile 8: | Zeile 15: | ||
In der Grafik sind nun folgende Mobilfunkverträge dargestellt: | In der Grafik sind nun folgende Mobilfunkverträge dargestellt: | ||
| − | |||
| − | |||
| − | |||
::::::::::[[Bild:Handytarife.png|450px]] | ::::::::::[[Bild:Handytarife.png|450px]] | ||
<br /><br /> | <br /><br /> | ||
Version vom 9. November 2009, 16:13 Uhr
"Handytarife"
Um euch das Thema etwas näher zu bringen, wollen wir einen linearen Zusammenhang zunächst an einem Beispiel veranschaulichen, auf das wir im Laufe des Lernpfades gelegentlich zurückkommen werden.
| Noch einmal kurz zur Wiederholung:
Proportionale Zuordnungen solltet ihr im Unterricht bereits besprochen haben. Eine solche Zuordnung liegt dann vor, wenn sich zwei Größen zueinander proportional verhalten. Das heißt sie steigen bzw. fallen im gleichen Verhältnis und haben somit immer einen konstanten Quotienten q=2. Größe / 1. Größe. (verdoppelt sich z.B. der Wert der x-Koordinate, so verdopplet sich auch der Wert der y-Koordinate) |
Nun zum Beispiel:
Der Mobilfunkanbieter "Smartphone" bietet seinen Kunden verschiedene Handyverträge an. Je nachdem ob ein Nutzer viel oder wenig telefoniert, soll für jeden ein passender Vertrag dabei sein, der ihm an seine Bedürfnisse angepasste Vorteile bietet.
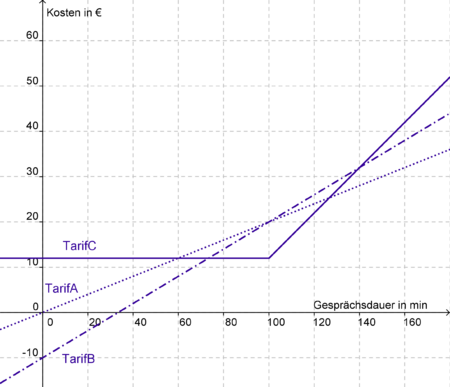
In der Grafik sind nun folgende Mobilfunkverträge dargestellt:
→ Beide Grafen der Mobilfunkverträge beschreiben einen linearen Zusammenhang, da das Verhältnis zwischen Kosten und telefonierter Minuten immer das gleiche ist. Zu beachten ist, dass Tarif A aus zwei Grafen, also zwei verschiedenen Funktionen, zusammengesetzt ist, die aber beide jeweils in ihren Größen proportional sind.
Arbeitsauftrag: Versuche die jeweiligen Vor- und Nachteile der drei Verträge zu beschreiben! Wie hoch ist jeweils die Grundgebühr? Wie hoch die Minutenpreise?
Arbeitsauftrag:
- Tarif A: keine Grundgebühr, der Minutenpreis beträgt 0,20 €
- (leicht abzulesen, da bei 100 Minuten die Kosten bei 20 € sind; der Bruch
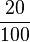lässt sich dann vereinfachen, sodass man auf 0,20 € pro Minute kommt)
- Tarif B: keine Grundgebühr, bis zur ca. 35. Minute telefoniert man kostenlos, der Minutenpreis beträgt dann ungefähr 0,29 €
- (es gibt verschiedene Möglichkeiten auf diesen Wert zu kommen; z.B. einfach den Grafen nach oben "verschieben", sodass er durch den Ursprung verläuft. Dann liegen die Kosten bei 140 Minuten bei genau 40 €; in den Taschenrechner eingegeben kommt man so auf den gerundeten Dezimalbruch 0,29 € pro Minute)
- Tarif C: die Grundgebühr beträgt 12 € (ungefähr abgelesen), der Minutenpreis danach 0,50 €
- (hierzu stellt man sich den Grafen wieder etwas nach unten "verschoben" vor; dann ist leicht zu sehen, dass der Preis pro 20 Minuten 10 € beträgt)
