HA: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Hausaufgabe 22.09.2009) |
(layout) |
||
| Zeile 1: | Zeile 1: | ||
| − | == | + | __NOTOC__ |
| − | [[Bild:S.161.12.png]] | + | |
| − | == | + | ==== 28.09.09 Seite 161_12 ==== |
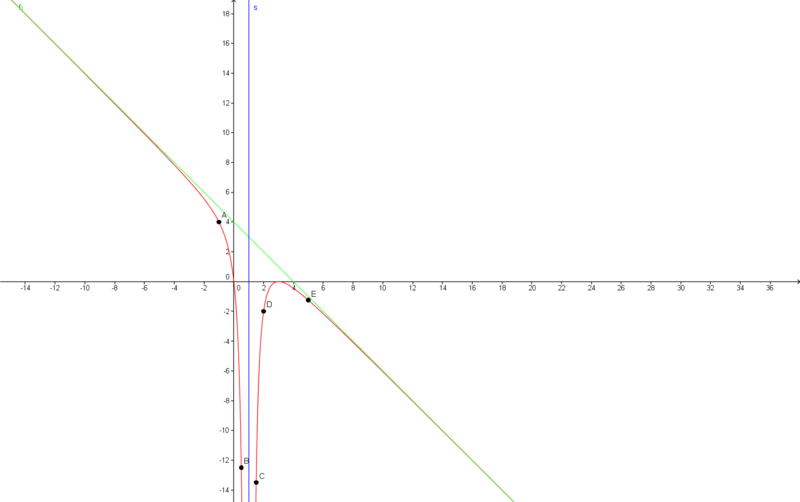
| + | [[Bild:S.161.12.png|800px]] | ||
| + | |||
| + | |||
| + | ==== 22.09.09 ==== | ||
*[[Media:161_10.pdf|Seite 161_10 Benjamin Schleicher]] | *[[Media:161_10.pdf|Seite 161_10 Benjamin Schleicher]] | ||
*[[LK Mathematik 2008 10/Lösungen Infinitesimalrechnung/HA1|Arbeitsblatt 3/Nr. 8 Philipp Issle]] | *[[LK Mathematik 2008 10/Lösungen Infinitesimalrechnung/HA1|Arbeitsblatt 3/Nr. 8 Philipp Issle]] | ||
| − | |||
| − | |||
| − | + | ||
| − | + | ==== 9.10.2008 Arbeitsblatt 3/Nr. 2 ==== | |
| + | |||
| + | Die Parabel -1/4x²+2x schließt mit der y-Achse und der Tangente im Kurvenpunkt P<sub>0</sub> (6;?) | ||
| + | ein Flächenstück vollständig ein. Wie groß ist diese Fläche? | ||
; Lösung | ; Lösung | ||
| Zeile 28: | Zeile 33: | ||
[[Bild:möööööp.png]] | [[Bild:möööööp.png]] | ||
| − | + | ;Arbeitsblatt 3/Nr. 5 | |
| − | + | ||
d) Für welchen Wert von a liegt zwischen G<sub>p</sub> und G<sub>g</sub><sub>a</sub> keine Fläche? Welche besondere Lage hat dann G<sub>p</sub> zu G<sub>g</sub><sub>a</sub>? | d) Für welchen Wert von a liegt zwischen G<sub>p</sub> und G<sub>g</sub><sub>a</sub> keine Fläche? Welche besondere Lage hat dann G<sub>p</sub> zu G<sub>g</sub><sub>a</sub>? | ||
| − | |||
| − | === | + | ==== 6.10.2008 ==== |
| + | |||
| + | ;Aufgabe 1 | ||
'''1.Bestimmen der Schnittpunkte:''' | '''1.Bestimmen der Schnittpunkte:''' | ||
| Zeile 48: | Zeile 54: | ||
| − | |||
'''2.Berechnung des Integrals:''' | '''2.Berechnung des Integrals:''' | ||
Version vom 23. September 2009, 12:44 Uhr
28.09.09 Seite 161_12
22.09.09
9.10.2008 Arbeitsblatt 3/Nr. 2
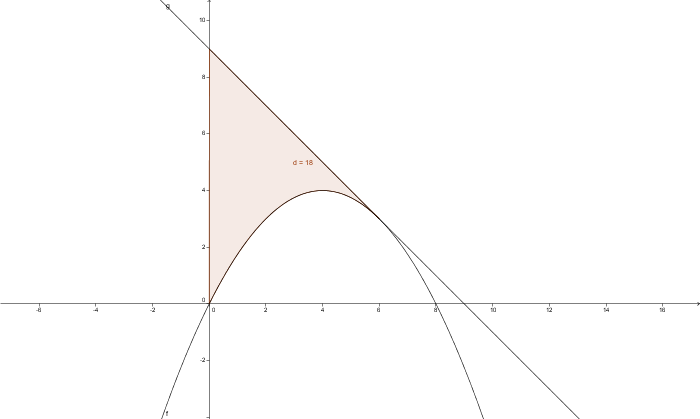
Die Parabel -1/4x²+2x schließt mit der y-Achse und der Tangente im Kurvenpunkt P0 (6;?) ein Flächenstück vollständig ein. Wie groß ist diese Fläche?
- Lösung
1. Tangente
f'(x)=-1/2x+2
f'(6)=-1 =>y=-1*6+t
f(6)= 3 => 3=-1*6 +t => t=9
y=-x+9
2. Flächenberechnung
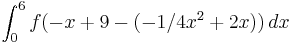
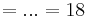
- Arbeitsblatt 3/Nr. 5
d) Für welchen Wert von a liegt zwischen Gp und Gga keine Fläche? Welche besondere Lage hat dann Gp zu Gga?
6.10.2008
- Aufgabe 1
1.Bestimmen der Schnittpunkte:
f(x)=0;
a * x - b * x3 = 0;
x (a - b * x2)=0
--> Mitternachtsformel: x1= 0; x2= 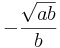 ; x3=
; x3= 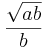
2.Berechnung des Integrals:
F(x)=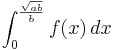 = ... =
= ... =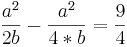
I. 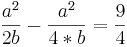
II. f´(1) = 0 ; a - 3b = 0; a = 3b eingesetzt in I.: b = 1 → a = 3
Seite 92/Nr. 33
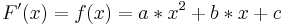
1. F hat Extremum in x = 5, d.h. f(5) = 0
25 a + 5 b + c = 0
2. f (1) = 4/7
a + b + c = 4/7
3. F hat Nullstelle in x = 3, d.h. F(3)=0
3 a + 3/2 b + c = 0
Ergebnis: a = 1/2; b = -22/7; c = 45/14