Benutzer:Lukas Bauernschubert: Unterschied zwischen den Versionen
(→Tipps:) |
|||
| Zeile 42: | Zeile 42: | ||
d)4<math>\frac{1}{2}</math>cm³-2<math>\frac{1}{5}</math>cm³=4,5cm³-2,2cm³=2,3cm³ | d)4<math>\frac{1}{2}</math>cm³-2<math>\frac{1}{5}</math>cm³=4,5cm³-2,2cm³=2,3cm³ | ||
| − | e)1<math>\frac{5}{8}</math>cm³+<math>\frac{3}{5}</math>cm³= | + | e)1<math>\frac{5}{8}</math>cm³+<math>\frac{3}{5}</math>cm³=1,625cm³+0,6cm³=2,225dm³ |
f)7,2l-1<math>\frac{3}{4}</math>dm³= | f)7,2l-1<math>\frac{3}{4}</math>dm³= | ||
Version vom 11. Mai 2009, 19:57 Uhr
Servus, ich bin der Lukas und finde es am Gymnasium toll. Meine Hobbys sind:Skifahren,Fußballspielen und schwimmen.Ich bin in der Klasse 6b.Mein Lieblingsfächer sind Latein (Herr Brech) und Mathe (Frau Schellmann).
Hier geht es zum Jahr der Mathematik:Jahr der Mathematik
Zuordnung
Ordne die Brüche den richtigen Oberbegriffen zu(Achtung Schwierig unten sind Tipps).
| Dezimalbruch endlich |  |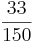
 |
 |
 |
 |
 |
|
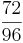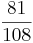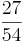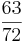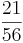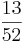
| Dezimalbruch unendlich |  |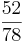
 |
 |
 |
 |
 |
|
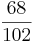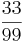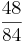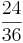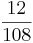
Tipps:
Erst vollständig kürzen (Am Besten mit Zettel und Stift)
So erkennt man einen unendlichen Dezimalbruch: Nur Brüche, deren Nenner nach dem vollständigen Kürzen keine anderen Primfaktoren als 2 und 5 enthalten, ergeben einen endlichen Dezimalbruch.
Lösungen zu S.136/26:
a)2
m³-
m³=2,8m³-0,5m³=2,3m³
b)hl+20m³= 0,8hl+20000dm³= 80l+20000l=20080l
c)
ml+0,125dm³= 0,6ml+125ml= 125,6ml
d)4cm³-2
cm³=4,5cm³-2,2cm³=2,3cm³
e)1
cm³+cm³=1,625cm³+0,6cm³=2,225dm³
f)7,2l-1
dm³=
g)5x(2
m³+1m³)=
h)1m³x0,8-2
l=
