Lernpfad zur zentrischen Streckung und den Ähnlichkeitssätzen/Zentrische Streckung: Unterschied zwischen den Versionen
(→Die Zentrische Streckung) |
(→Die Zentrische Streckung) |
||
| Zeile 17: | Zeile 17: | ||
Bei einer Zentrischen Streckung mit dem Streckzentrum Z und dem Streckfaktor k (k > 0) gilt für den Bildpunkt A zu einem Punkt P (P ungleich Z): | Bei einer Zentrischen Streckung mit dem Streckzentrum Z und dem Streckfaktor k (k > 0) gilt für den Bildpunkt A zu einem Punkt P (P ungleich Z): | ||
# A liegt auf der von Z ausgehenden Halbgeraden durch P | # A liegt auf der von Z ausgehenden Halbgeraden durch P | ||
| − | # <math>\overline{ZA} = \overline{ZP} \ | + | # <math>{\overline{ZA} = k \cdot \overline{ZP}\,}</math> |
</div> | </div> | ||
Version vom 20. Januar 2009, 19:46 Uhr
Die Zentrische Streckung
|
Bei der bisher behandelten Abbildungen, wie Achsenspiegelung, Drehung, Verschiebung, die unter dem Namen Kongruenzabbildungen zusammengefasst werden, blieb die Größe unverändert. |
Merke:
Bei einer Zentrischen Streckung mit dem Streckzentrum Z und dem Streckfaktor k (k > 0) gilt für den Bildpunkt A zu einem Punkt P (P ungleich Z):
- A liegt auf der von Z ausgehenden Halbgeraden durch P
-
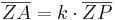
Eigenschaften der Zentrischen Streckung:
- Die Zentrische Streckung ist eine geradentreue Abbildung. Jede Gerade, die nicht durch das Streckzentrum verläuft wird auf eine zu ihr parallele Bildgerade abgebildet. z.B.
- Die Zentrische Streckung ist verhältnistreu. Jede Urstrecke wird auf eine parallele Bildstrecke der k - fachen Länge abgebildet. z.B.
- Die Zentrische Streckung ist eine winkeltreue Abbildung. Jeder Winkel wird auf einen gleich großen Winkel abgebildet. z.B.
- Die Bildfigur hat den k2 - fachen Flächeninhalt der Originalfigur. z.B.
Die nachfolgende Abbildung zeigt die Zentrische Streckung eines Fünfeckes. Mit Hilfe der Maus kannst du die Punkte verschieben.
Arbeitsauftrag:
Zeichne den Stadtplan unter der Überschrift "Die Zentrische Streckung" verkleinert in dein Heft und schreibe die Merksätze daneben.


