|
|
| Zeile 1: |
Zeile 1: |
| | <div style="border: 1px solid #dfdfdf; background-color:#F5F5F5; align:center; padding:4px;"> | | <div style="border: 1px solid #dfdfdf; background-color:#F5F5F5; align:center; padding:4px;"> |
| | == Sozialkunde == | | == Sozialkunde == |
| | + | [[Bild:Parteien-verbaende.gif]] |
| | | | |
| | == Mathematik == | | == Mathematik == |
Version vom 7. November 2007, 16:10 Uhr
Umfang
Der Pi-Song 1
- Messt von verschiedenen runden Gegenständen (z.B. Eimer, Teller, Tasse, Glas, Dose, CD, Münze, ...) jeweils den Durchmesser d und den Umfang U möglichst genau ab und notiert die Messungen in einer Tabelle.
- Bestimmt U , d auch aus folgendem Bibeltext im ersten Buch der Könige (Kap.7, Ver 23): »Hierauf fertigte er ein kreisrundes Becken an, das von einem Rand zum anderen 10 Ellen maß...,eine Schnur von 30 Ellen umspannte es.«
- Ergänzt die Messwerte in der Tabelle, indem ihr weitere Werte aus diesem interaktiven Arbeitsblatt (Aufgaben 1 und 2) übernehmt.
- Was fällt euch auf?
- Stellt eure Messwerte in einem Koordinatensystem dar und vergleicht euer Ergebnis mit diesem Applet.
- Was kann man über den Zusammenhang zwischen dem Umfang und dem Durchmesser von Kreisen aussagen?. Schreibt eure Überlegungen auf.
- Bestimmt das Verhältnis U : d, rundet das Ergebnis auf zwei Stellen nach dem Komma und ergänzt eure Tabelle.
- Versuche, eine Formel aufzustellen, die den Zusammenhang zwischen dem Umfang und dem Durchmesser von Kreisen beschreibt.
- Erstellt eine übersichliche Folie mit euren Ergebnissen.
Schülerlösung
Lösung zum download
Für alle, die noch mehr wissen wollen: Artikel über Pi in Wikipedia
Hilfsmittel: Runde Gegenstände, Schnur, Maßband
|
Fläche
Der Pi-Song 2
- Kästchen zählen: Bestimme den Flächeninhalt dieses Kreises:
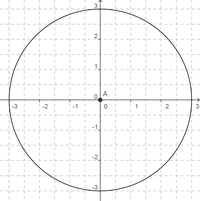 Klick dazu hier! Klick dazu hier!
- Zeichnet auf Millimeterpapier Kreise mit verschiedenen Radien r und bestimmt den Flächeninhalt A ebenfalls durch Kästchen zählen.
- Notiert eure Messungen in einer Tabelle.
- Stellt die Messwerte in einem Koordinatensystem dar und vergleicht eure Ergebnisse mit folgendem Applet
- Was kann man über den Zusammenhang zwischen dem Radius und der Fläche von Kreisen aussagen? Schreibt eure Überlegungen auf.
- Bestimmt das Verhältnis A : r², rundet das Ergebnis auf zwei Stellen nach dem Komma und ergänzt eure Tabelle.
- Versuche, eine Formel aufzustellen, die den Zusammenhang zwischen der Fläche und dem Radius von Kreisen beschreibt.
- Erstellt eine übersichtliche Folie mir euren Ergebnissen.
Hilfsmittel: Millimeterpapier, Zirkel
|
|
|
Links
Rechnen mit Potenzen
Fläche und Umfang des Kreises
|



