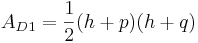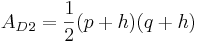Höhensatz: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Lösung zu Beweis und Arbeitsauftrag eingefügt) |
K (hat „Höhensatz 1“ nach „Lernpfad zur Satzgruppe des Pythagoras/Höhensatz 1“ verschoben: Bessere Übersicht) |
Version vom 29. November 2008, 11:48 Uhr
Der Höhensatz
Ein weiterer Satz aus der Satzgruppe des Pythagoras ist der Höhensatz.
Grafiken zu Beweis von Höhensatz:
Arbeitsauftrag:
- Zeichne die oben stehende Grafik in dein Heft und notiere dir die Bemerkungen zur Benennung der Seiten!
- Berechne den Flächeninhalt der beiden Dreiecke!
- Was fällt dir auf?
- Was kann man daraus folgern?
Fläche für Dreieck 1:
Fläche für Dreieck 2:
Folgerung:
- Die Dreiecke sind Flächengleich
- In beiden Dreiecken tauchen das rote und das gelbe Dreieck auf
- Der blaue Flächeninhalt in beiden Dreiecken muss also die gleiche Fläche haben, da:
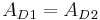
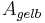 und
und 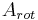 in beiden Dreiecken gleich
in beiden Dreiecken gleich
- Daraus folgt:
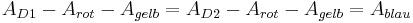
Da 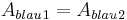 kann man sagen:
kann man sagen:
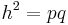
Du hast den Höhensatz bewiesen. Hier geht es nun zum Hefteintrag.