Benutzer:Hauck Anne: Unterschied zwischen den Versionen
Aus RMG-Wiki
K |
K |
||
| Zeile 8: | Zeile 8: | ||
1._)Bestimme die Nullstellen: | 1._)Bestimme die Nullstellen: | ||
f(x)=0 für ? | f(x)=0 für ? | ||
| − | \frac{-1}{3}x^2+2x+1=0 | + | <math>\frac{-1}{3}x^2+2x+1=0</math> |
\frac{-1}{3}(x^2-6x)=-1 | \frac{-1}{3}(x^2-6x)=-1 | ||
x^2-6x=3 | x^2-6x=3 | ||
Version vom 29. September 2008, 17:10 Uhr
Lösung der Hausaufgabe vom Aufgabenblatt 2 S.216/Nr.10
Aufgabenstellung:
Wie groß ist die Fläche, die vom Graphen Gf der Funktion f(x)=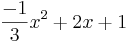
, der Ordinate des höchsten Punktes, der x-Achse und der y-Achse eingeschlossen wird?
Lösungsweg:
1._)Bestimme die Nullstellen:
f(x)=0 für ?\frac{-1}{3}(x^2-6x)=-1 x^2-6x=3 x^2-6x-3=0 x_{1/2}= \frac{-b^+_-\sqrt{b^2-4\cdota\cdotc}}{2\cdota}
2._)Bestimme das Integral von 0 bis zum x-Wert der Nullstelle, der in positiver x-Richtung liegt:
Veranschaulichung mit Geogebra Datei:Veranschaulichung AB2 S.216/Nr.10.jpg
