Abi 2017 Analysis I Teil A: Unterschied zwischen den Versionen
| Zeile 10: | Zeile 10: | ||
| − | <center>[https://www.isb.bayern.de/download/19427/abiturpruefung_mathematik_2017_pruefungsteil_a.pdf '''Download der Originalaufgaben'''] - [[Media: | + | <center>[https://www.isb.bayern.de/download/19427/abiturpruefung_mathematik_2017_pruefungsteil_a.pdf '''Download der Originalaufgaben'''] - [[Media:Lösung_Ana_2017_2_Teil_A.pdf|Lösung zum Ausdrucken]] </center> |
</td></tr></table></center> | </td></tr></table></center> | ||
Version vom 28. März 2018, 22:36 Uhr
|
|
Gegeben ist die Funktion a) Geben Sie Dg und die Koordinaten des Schnittpunkts von Gg mit der y-Achse an. b) Beschreiben Sie, wie Dg schrittweise aus dem Graphen der in IR0+
definierten Funktion
|
Eine Funktion f ist durch a) Ermitteln Sie die Nullstelle der Funktion f. b) Die Tangente an den Graphen von f im Punkt S(0 |1) begrenzt mit den beiden Koordinatenachsen ein Dreieck. Weisen Sie nach, dass dieses Dreieck gleichschenklig ist. |
Geben Sie jeweils den Term einer Funktion an, die über ihrer maximalen Definitionsmenge die angegebenen Eigenschaften besitzt. a) Der Graph der Funktion f ist achsensymmetrisch zur y-Achse und die Gerade mit der Gleichung x = 2 ist eine senkrechte Asymptote. b) Die Funktion g ist nicht konstant und es gilt |
An einer Messstation wurde über einen Zeitraum von 10 Stunden die Anzahl der Pollen in einem Kubikmeter Luft ermittelt. Dabei kann die Anzahl der Pollen in einem Kubikmeter Luft zum Zeitpunkt t (in Stunden nach Beginn der Messung) durch die Gleichung n(t)= 3t2 -60t+500 beschrieben werden. a) Bestimmen Sie die mittlere Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft während der ersten beiden Stunden der Messung. b) Ermitteln Sie den Zeitpunkt nach Beginn der Messung, zu dem die momentane Änderungsrate der Anzahl der Pollen in einem Kubikmeter Luft -30 1/h beträgt. |
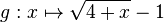 mit maximaler Definitionsmenge
Dg . Der Graph von g wird mit Gg bezeichnet.
mit maximaler Definitionsmenge
Dg . Der Graph von g wird mit Gg bezeichnet.
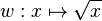 hervorgeht, und geben Sie die
Wertemenge von g an.
hervorgeht, und geben Sie die
Wertemenge von g an.

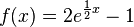 mit x ∈ IR gegeben.
mit x ∈ IR gegeben.