Abi 2016 Analysis I Teil B: Unterschied zwischen den Versionen
| Zeile 86: | Zeile 86: | ||
sind, in gleicher Höhe über | sind, in gleicher Höhe über | ||
dem Erdboden befestigt. Der | dem Erdboden befestigt. Der | ||
| − | Graph G<sub>f</sub> aus Aufgabe 1 | + | Graph G<sub>f</sub> aus Aufgabe 1 beschreibt im Bereich <math> |
| − | + | -4 \le x \ge 4 </math> modellhaft den Verlauf des | |
| − | -4 \le x \ge 4 </math> | + | Seils, wobei die Fußpunkte F<sub>1</sub> |
| − | modellhaft den Verlauf des | + | und F<sub>2</sub> der Masten durch die Punkte |
| − | Seils, wobei die Fußpunkte | + | (4\0) |
| − | F<sub>1</sub> | + | |
| − | und | + | |
| − | 2 | + | |
| − | + | ||
| − | + | ||
| − | Punkte | + | |
| − | + | ||
| − | 4 | + | |
| | ||
bzw. | bzw. | ||
Version vom 26. Juli 2017, 08:25 Uhr
|
|
Gegeben ist die in IR definierte Funktion a) Bestimmen Sie die Koordinaten des Schnittpunktes von Gf mit der y-Achse und begünden Sie, dass Gf oberhalb der x-Achse verläuft. b) Ermitteln Sie das Symmetrieverhalten von Gf sowie das Verhalten von f für x→-∞ x→+∞. c)
Zeigen Sie, dass für die zweite Ableitung f von f die Beziehung d) e) f) g) h) |
a)Die Enden eines Seils werden
an zwei vertikalen Masten, die
8,00 m voneinander entfernt
sind, in gleicher Höhe über
dem Erdboden befestigt. Der
Graph Gf aus Aufgabe 1 beschreibt im Bereich bzw. 4|0 dargestellt werden (vgl. Abbildung) . Eine Längeneinheit im Koordinaten- system entspricht einem Meter in der Realität. b) c) d) |
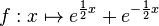 . Der Graph von f wird
mit Gf bezeichnet.
. Der Graph von f wird
mit Gf bezeichnet.
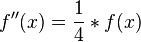 für x∈IR gilt. Weisen Sie nach, dass Gf linksgekrümmt ist. (Zur Kontrolle
für x∈IR gilt. Weisen Sie nach, dass Gf linksgekrümmt ist. (Zur Kontrolle 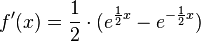 )
)
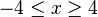 modellhaft den Verlauf des
Seils, wobei die Fußpunkte F1
und F2 der Masten durch die Punkte
(4\0)
modellhaft den Verlauf des
Seils, wobei die Fußpunkte F1
und F2 der Masten durch die Punkte
(4\0)

