Abi 2014 Analysis II Teil B: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „__NOTOC__ <div style="padding:1px;background: #EEEEE6;border:0px groove;"> <center><table border="0" width="800px" cellpadding=5 cellspacing=15> <tr><td wid…“) |
|||
| Zeile 20: | Zeile 20: | ||
<center><table border="0" width="800px" cellpadding=5 cellspacing=15> | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | Gegeben ist die Funktion f mit <math>f(x) = \frac{20x}{x^2-25}</math> und maximalem Definitionsbereich D<sub>f</sub>. Die Abbildung zeigt einen Teil des Graphen G<sub>f</sub> von f. | ||
| + | |||
| + | '''"Graph einfuegen!"''' | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| + | a) Zeigen Sie, dass D<sub>f</sub>=IR \ {-5;5} gilt und dass G<sub>f</sub> symmetrisch bezüglich des Koordinatenursprungs ist. Geben Sie die Nullstelle von f sowie die Gleichungen der drei Asymptoten von G<sub>f</sub> an. | ||
| + | |||
| + | b) Weisen Sie nach, dass die Steigung von G<sub>f</sub> in jedem Punkt des Graphen negativ ist. Berechnen Sie die Größe des Winkels, unter dem G<sub>f</sub> die x-Achse schneidet. | ||
| + | |||
| + | c) Skizzieren Sie in der Abbildung den darin fehlenden Teil von G<sub>f</sub> unter Berücksichtigung der bisherigen Ergebnisse. | ||
| + | |||
| + | d) Die Funktion <math>f^* : x \mapsto f(x)</math> mit Definitionsbereich ]5;+∞[ unterscheidet sich von der Funktion f nur hinsichtlich des Definitionsbereichs. Begründen Sie, dass die Funktion f nicht umkehrbar ist, die Funktion f* dagegen schon. Zeichnen Sie den Graphen der Umkehrfunktion von f* in die Abbildung ein. | ||
| + | |||
| + | e) Der Graph von f, die x-Achse sowie die Geraden mit den Gleichungen x=10 und x=s mit s>10 schließen ein Flächenstück mit dem Inhalt A(s) ein. Bestimmen Sie A(s). | ||
| + | |||
| + | (Ergebnis: <math>A(s) = 10 \cdot ln\frac{s^2-25}{75}</math> ) | ||
| + | |||
| + | f) Ermitteln Sie s so, dass das Flächenstück aus Aufgabe 1e den Inhalt 100 besitzt. | ||
| + | |||
| + | g) Bestimmen Sie das Verhalten von A(s) für s→+∞ . | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Version vom 8. Juli 2017, 14:13 Uhr
|
|
|
Gegeben ist die Funktion f mit "Graph einfuegen!"
a) Zeigen Sie, dass Df=IR \ {-5;5} gilt und dass Gf symmetrisch bezüglich des Koordinatenursprungs ist. Geben Sie die Nullstelle von f sowie die Gleichungen der drei Asymptoten von Gf an. b) Weisen Sie nach, dass die Steigung von Gf in jedem Punkt des Graphen negativ ist. Berechnen Sie die Größe des Winkels, unter dem Gf die x-Achse schneidet. c) Skizzieren Sie in der Abbildung den darin fehlenden Teil von Gf unter Berücksichtigung der bisherigen Ergebnisse. d) Die Funktion e) Der Graph von f, die x-Achse sowie die Geraden mit den Gleichungen x=10 und x=s mit s>10 schließen ein Flächenstück mit dem Inhalt A(s) ein. Bestimmen Sie A(s). (Ergebnis: f) Ermitteln Sie s so, dass das Flächenstück aus Aufgabe 1e den Inhalt 100 besitzt. g) Bestimmen Sie das Verhalten von A(s) für s→+∞ .
|
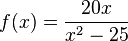und maximalem Definitionsbereich Df. Die Abbildung zeigt einen Teil des Graphen Gf von f.
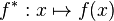mit Definitionsbereich ]5;+∞[ unterscheidet sich von der Funktion f nur hinsichtlich des Definitionsbereichs. Begründen Sie, dass die Funktion f nicht umkehrbar ist, die Funktion f* dagegen schon. Zeichnen Sie den Graphen der Umkehrfunktion von f* in die Abbildung ein.
)
|
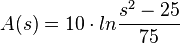