Funktionen: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
| − | <div style="padding:1px;background: # | + | <div style="padding:1px;background: #ABAABF;border:0px groove;"> |
| − | <center><table border="0" width=" | + | <center><table border="0" width="1000px" cellpadding=2 cellspacing=2> |
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | + | ||
| + | == Teste dein Wissen== | ||
| + | Um die folgenden Aufgaben lösen zu können , solltest du mit folgenden Funktionen umgehen können: <br/> | ||
| + | - Lineare Funktionen <br/> | ||
| + | - Quadratische Funktionen <br/> | ||
| + | - Potenzfunktionen/Ganzrationale Funktionen (höheren Grades) <br/> | ||
| + | - Gebrochen-Rationale Funktionen <br/> | ||
| + | - Exponentialfunktionen <br/> | ||
| + | - Trigonometrische Funktionen <br/> | ||
| + | In den Übungen werden die verschiedenen Funktionstypen gemischt.<br/> | ||
| + | <br/> | ||
| + | |||
1) Ordne Funktionstyp, Funktionsterm und Funktionsgraph passend zu. <br/> | 1) Ordne Funktionstyp, Funktionsterm und Funktionsgraph passend zu. <br/> | ||
<div class="zuordnungs-quiz"> | <div class="zuordnungs-quiz"> | ||
Version vom 1. September 2014, 21:00 Uhr
|
Teste dein WissenUm die folgenden Aufgaben lösen zu können , solltest du mit folgenden Funktionen umgehen können: 1) Ordne Funktionstyp, Funktionsterm und Funktionsgraph passend zu.
Entscheide, ob P(3/-6) auf dem Graphen der Funktion 3) Gib den Funktionsterm einer Geraden durch P(1/5) an, die parallel zur Geraden g: y=2x+4 verläuft. p(x)= 2x+3 () 4) Kreuze für
|
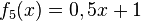
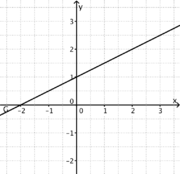
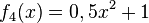
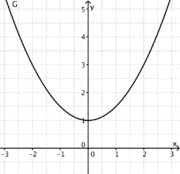
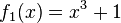
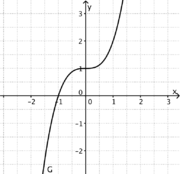
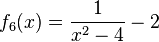
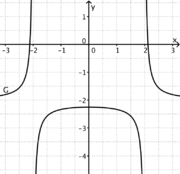
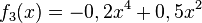
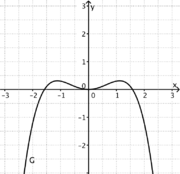
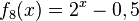
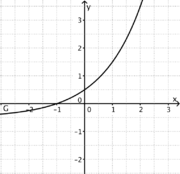
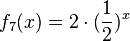
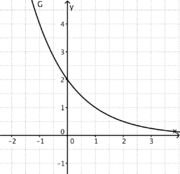
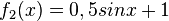
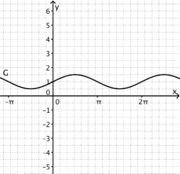
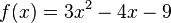 liegt.
(Nein, P liegt unterhalb von Gf)
(!Nein, P liegt oberhalb von Gf)
(!Ja, P liegt auf Gf)
liegt.
(Nein, P liegt unterhalb von Gf)
(!Nein, P liegt oberhalb von Gf)
(!Ja, P liegt auf Gf)
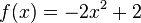 die richtige Aussage an:
Versuche die Aufgabe durch Überlegen zu lösen; es sind keine Berechnungen nötig
(Gf ist weiter als die Normalparabel)
(!Gf ist enger als die Normalparabel)
(!Gf hat die Form einer Normalparabel)
(Gf hat zwei Schnittpunkte mit der x-Achse)
(!Gf hat einen Schnittpunkt mit der x-Achse)
(!Gf hat keinen Schnittpunkt mit der x-Achse)
(!Gf ist punktsymmetrisch bzgl des Ursprungs)
(Gf ist achsensymmetrisch bzgl des y-Achse)
(!Gf ist nicht symmetrisch)
(!Der Grenzwert für x gegen unendlich ist 0)
(Der Grenzwert für x gegen unendlich ist unendlich)
(!Der Grenzwert für x gegen minus unendlich ist unendlich)
die richtige Aussage an:
Versuche die Aufgabe durch Überlegen zu lösen; es sind keine Berechnungen nötig
(Gf ist weiter als die Normalparabel)
(!Gf ist enger als die Normalparabel)
(!Gf hat die Form einer Normalparabel)
(Gf hat zwei Schnittpunkte mit der x-Achse)
(!Gf hat einen Schnittpunkt mit der x-Achse)
(!Gf hat keinen Schnittpunkt mit der x-Achse)
(!Gf ist punktsymmetrisch bzgl des Ursprungs)
(Gf ist achsensymmetrisch bzgl des y-Achse)
(!Gf ist nicht symmetrisch)
(!Der Grenzwert für x gegen unendlich ist 0)
(Der Grenzwert für x gegen unendlich ist unendlich)
(!Der Grenzwert für x gegen minus unendlich ist unendlich)

