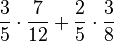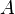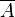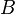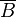Stochastik: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: „test“) |
|||
| Zeile 1: | Zeile 1: | ||
| − | + | __NOTOC__ | |
| + | <div style="background: #ABAABF"> | ||
| + | |||
| + | <center><table border=0 width="800px" cellpadding=5 cellspacing=5> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | |||
| + | {| | ||
| + | |width="60%"| | ||
| + | |||
| + | == Teste dein Wissen== | ||
| + | |||
| + | In einem Eimer liegen 15 rote, und 10 gelbe Tulpenzwiebeln. Diese sind von außen nicht unterscheidbar; später werden sie jedoch verschieden farbig blühen. Es werden nacheinander zwei Zwiebeln gezogen und in eine Reihe gesteckt. | ||
| + | a) Ordne dieser Sachsituation ein Baumdiagramm zu. Begründe deine Entscheidung. | ||
| + | <div class="multiplechoice-quiz"> | ||
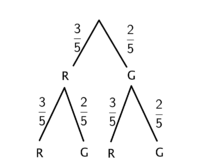
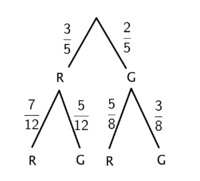
| + | [[Datei:Baumdiagramm1.png|thumb|Baumdiagramm 1|links|200px]] [[Datei:Baumdiagramm2.png|thumb|Baumdiagramm 2|zentriert|200px]] | ||
| + | (! Baumdiagramm 1) (Baumdiagramm 2) | ||
| + | </div> | ||
| + | <popup name="Begründung"> | ||
| + | Da die Zwiebeln nach dem Ziehen nicht zurückgelegt werden, verändert sich beim zweiten Zug die Wahrscheinlichkeit eine rote oder gelbe Zwiebeln zu ziehen. | ||
| + | </popup> <br /> | ||
| + | |||
| + | b) Peter berechnet, dass die Wahrscheinlichkeit für zwei gleichfarbige Blumen 50% beträgt. Beschreibe in Worten ein richtiges Vorgehen, um auf den Wert zu gelangen. | ||
| + | <popup name="Lösung"> | ||
| + | Um die Wahrscheinlichkeit für das Ereignis "gleichfarbige Blumen" zu berechnen, müssen zunächst mit Hilfe der ersten Pfadregel die Wahrscheinlichkeiten für die Ergebnisse "Rot-Rot" und "Gelb-Gelb" berechnet werden. Dafür müssen die Wahrscheinlichkeiten entlang der Äste multipliziert werden. Im Anschluss werden diese beiden Wahrscheinlichkeiten addiert, dies ist die zweite Pfadregel. | ||
| + | P("gleichfarbig") = P(RR)+P(GG) = <math> \frac35 \cdot \frac{7}{12} + \frac25 \cdot \frac38 </math> | ||
| + | |||
| + | </popup> <br /> | ||
| + | |||
| + | 15) Nebenstehende Vierfeldertafel gehört zu einem zweistufigen Zufallsexperiment mit den zwei Ereignissen A und B. | ||
| + | a. Fülle die Vierfeldertafel vollständig aus. <br/> | ||
| + | |||
| + | {| class="wikitable center" | ||
| + | |- | ||
| + | | ||<math>A</math>||<math> \overline{A} </math>|| | ||
| + | |- | ||
| + | | <math>B</math> || 0,15 || 0,4 || {0,55} | ||
| + | |- | ||
| + | | <math> \overline{B} </math> || {0,05} || {0,4} || {0,45} | ||
| + | |– | ||
| + | | || 0,2 || {0,8} || {1} | ||
| + | |} | ||
Version vom 11. September 2014, 10:50 Uhr
|
|