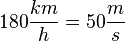Geschwindigkeit: Unterschied zwischen den Versionen
K (→) |
K (→) |
||
| Zeile 67: | Zeile 67: | ||
| − | "<math> \Delta </math> s" bedeutet "Streckenabschnitt am Ende" minus "Streckenabschnitt am Anfang". (Das ist wichtig, wenn wir wie in Aufgabe 1c) die Geschwindigkeit in den letzten 6 Metern der Bewegung des Pkws ausrechnen wollen: <br /> | + | "<math> \Delta </math> s" bedeutet "Streckenabschnitt am Ende" minus "Streckenabschnitt am Anfang" des betrachteten Zeitintervalls. <big><span style="color:#C00000"> ''' (Hefteintrag: Diese Zeile bis hier)'''</span> </big> (Das ist wichtig, wenn wir wie in Aufgabe 1c) die Geschwindigkeit in den letzten 6 Metern der Bewegung des Pkws ausrechnen wollen: <br /> |
<math> \Delta </math> s = 12m-6m = 6m) <br /> | <math> \Delta </math> s = 12m-6m = 6m) <br /> | ||
<br /> | <br /> | ||
Version vom 6. Januar 2014, 22:25 Uhr
|
Einführung:
|
Geschwindigkeit Ein weiteres Beispiel: Also wie kann man nun die Geschwindigkeit berechnen?
Möchte man die durchschnittliche Geschwindigkeit eines Körpers berechnen, so dividiert man die zurückgelegte Strecke durch die dafür benötigte Zeit. Aufgabe 1: a) Berechne mit Hilfe des Videos die durchschnittliche Geschwindigkeit des Pkws insgesamt. b) Berechne nun die durchschnittliche Geschwindigkeit des Pkws auf den ersten 6 Metern. c) Wie kannst du die Geschwindigkeit auf den letzten 6 Metern ausrechnen? Versuche eine allgemeine Formel anzugeben.
Umrechnung von
Bei der Umrechnung von Bei der Umrechnung von Faustformel: "Der kleinere Wert ist in
|
? 
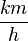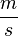anzugeben. Das Erbebnis weißt du doch bestimmt!
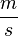
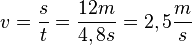
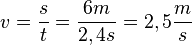
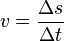(Gesprochen: 
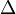delta) 
≈ 
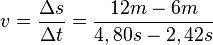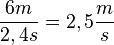
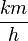und umgekehrt
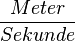oder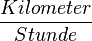 
In der Physik bietet sich meistens die 1. Darstellung an, während du im Alltag meistens mit der 2. Darstellung konfrontiert wirst.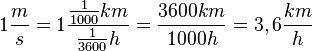 
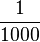km und 1 Sekunde ist 
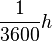(1h sind 60min mit jeweils 60s); am Ende noch durch den Bruch teilen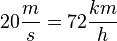 
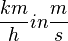muss man den Wert durch 3,6 teilen und anschließend die Einheit ändern: Z.B. 
