Flächenberechnung: Unterschied zwischen den Versionen
| Zeile 24: | Zeile 24: | ||
(Seite b des Rechtecks <math>\widehat{=}</math> h<sub>c</sub>) (!Seite b des Rechtecks <math>\widehat{=}</math> Seite b des <math>\Delta</math>) | (Seite b des Rechtecks <math>\widehat{=}</math> h<sub>c</sub>) (!Seite b des Rechtecks <math>\widehat{=}</math> Seite b des <math>\Delta</math>) | ||
| − | '''Wie lautet die Formel für das | + | '''Wie lautet die Formel für das Rechteck ausgedrückt durch c und h<sub>c</sub>?''' |
(A = c<math>\cdot</math>h<sub>c</sub>) (!A = c<math>\cdot</math>h<sub>c</sub><math>\cdot</math>4) | (A = c<math>\cdot</math>h<sub>c</sub>) (!A = c<math>\cdot</math>h<sub>c</sub><math>\cdot</math>4) | ||
Version vom 12. September 2010, 16:32 Uhr
Die Fläche des Dreiecks
Arbeitsaufträge:
- Ziehe die Dreiecke bei A und B so, dass du eine rechteckige Fläche bekommst, die du berechnen kannst.
- Beantworte die Fragen und versuche die Flächenformel für das Dreieck herzuleiten.
- Wenn du Fehler hast beginne von vorne.
Wie heißt die neue Fläche? (Rechteck) (!Kreis)
Wie berechnest du den Flächeninhalt eines Rechtecks?
(A = a 
b) (!A = ab2)
Welche Seite des Dreiecks entspricht der Seite a des Rechtecks?
(Seite a des Rechtecks 
Seite c des 
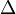) (!Seite a des Rechtecks Seite a des )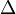
Welches Teil des Dreiecks entspricht der Seite b des Rechtecks?
(Seite b des Rechtecks hc) (!Seite b des Rechtecks Seite b des )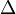
Wie lautet die Formel für das Rechteck ausgedrückt durch c und hc?
(A = chc) (!A = chc4)
Welcher Zusammenhang besteht zwischen der Größe der Fläche des 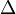und der des Rechtecks?
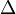( ist halb so groß) (! 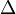ist doppelt so groß)
Wie musst du bei der Hälfte rechnen?
(: 2) (!2)
Die Flächenformel für das Dreieck lautet:
(!chc) (chc : 2) (!c + hc) (!c + hc : 2) (!2chc)
Wenn du Fehler hast, drücke F5 und beginne diese Seite von vorne.
Hier kommst du zu einer Übungsaufgabe.
