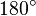Dreieck: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 20: | Zeile 20: | ||
*Die '''Verbindungsstrecken''' zwischen den Punkten heißen '''Seiten'''. Die '''Seite''', die einer '''Ecke gegenüberliegt''' wird '''a, b oder c''' genannt. Seite '''a liegt dem Eckpunkt A''' gegenüber, Seite '''b dem Punkt B''', Seite '''c dem Punkt C''' | *Die '''Verbindungsstrecken''' zwischen den Punkten heißen '''Seiten'''. Die '''Seite''', die einer '''Ecke gegenüberliegt''' wird '''a, b oder c''' genannt. Seite '''a liegt dem Eckpunkt A''' gegenüber, Seite '''b dem Punkt B''', Seite '''c dem Punkt C''' | ||
*Die '''Winkel''' werden '''<math>\alpha</math>, <math>\beta</math> und <math>\gamma</math>''' genannt. '''<math>\alpha</math> ist der Winkel am Eckpunkt A''', '''<math>\beta</math> bei B''' und '''<math>\gamma</math> bei C''' | *Die '''Winkel''' werden '''<math>\alpha</math>, <math>\beta</math> und <math>\gamma</math>''' genannt. '''<math>\alpha</math> ist der Winkel am Eckpunkt A''', '''<math>\beta</math> bei B''' und '''<math>\gamma</math> bei C''' | ||
| − | *Die Summe der Innenwinkel beträgt <math>180^\circ</math> | + | *Die Summe der Innenwinkel beträgt <math>\alpha</math> + <math>\beta</math> + <math>\gamma</math> = <math>180^\circ</math> |
| [[Bild:Dreieck allgemein.jpg]] | | [[Bild:Dreieck allgemein.jpg]] | ||
|} | |} | ||
Version vom 9. September 2010, 15:08 Uhr
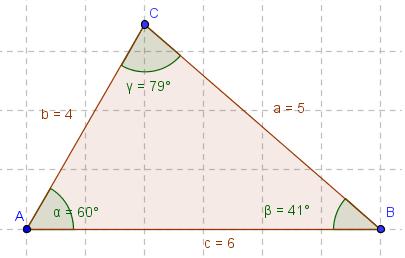
Das allgemeine Dreieck
Arbeitsauftrag:
- Zeiche das nebenstehende Dreieck in dein Heft und beschrifte es wie in der Grafik.
- Tipp
- Zeichne zunächst die Seite c, trage dann den Winkel
 an und zuletzt die Seite b.
an und zuletzt die Seite b.
- Übernimm auch die Eigenschaften eines Dreiecks.
Hier kommst du zur nächsten Übung.
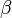 und
und 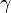 genannt.
genannt.