2007 VI: Unterschied zwischen den Versionen

Version vom 2. März 2010, 14:11 Uhr

Leistungskurs Mathematik (Bayern): Abiturprüfung 2007 Analytische Geometrie VI

Lösungen erstellt von: Johanna Buchner, Isabell Geist und Ann Christin Werner
Angabe

In einem kartesischen Koordinatensystem des IR³ ist die Ebenenschar E_t : 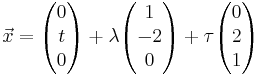$\vec x = \begin{pmatrix} 0 \\ t \\ 0 \end{pmatrix} + \lambda\begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix} + \tau\begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix}$ mit λ, τ є IR und t є IR gegeben.

Aufgabe 1

a) Bestimmen Sie eine Gleichung von E_t in Normalenform. Begründen Sie, dass alle Ebenen der Schar zueinander parallel sind.

[mögliches Teilergebnis: E_t : 2x₁ + x₂ - 2x₃ - t = 0]

b) Berechnen Sie den Winkel φ, unter dem jede Ebene der Schar E_t die x₁x₂-Ebene schneidet, auf eine Dezimale gerundet.

c) Die Ebene L enthält die x₂-Achse und ist Lotebene zur Ebene E_t. Ermitteln Sie eine Gleichung von L in Normalenform und geben Sie eine Gleichung der Schnittgeraden s_t von L und E_t in Parameterform an.

[mögliches Teilergebnis: L: x₁ + x₃ = 0]

Aufgabe 2

Die Ebene E_t schneidet die x₁-Achse im Punkt A_t, die x₂-Achse im Punkt B_t und die x₃-Achse im Punkt C_t. Diese Punkte und der Ursprung O sind für t ≠ 0 die Ecken einer Pyramide II_t.

a) Berechnen Sie die Koordinaten der Punkte A_t, B_t und C_t und zeichnen Sie in einem Koordinatensystem für t = -8 die Pyramide II_-8 ein.

[Teilergebnis: A_t (0,5t|0|0); B_t (0|t|0); C_t (0|0|-0,5t)]

Andere Lösung

Man hätte die Achsengeraden aufstellen können, mit dem Ursprung als Aufpunkt 
und dem jeweiligen  Richtungsvektor und dann den jeweiligen allg. Geradenpunkt
in die Ebene einsetzen können.

b) Zeigen Sie, dass die Pyramide II_t den Oberflächeninhalt t² besitzt, und ermitteln Sie das Volumen V_t von II_t in Abhängigkeit von t.

c) Die Ebene F : 2x₂ = t liegt parallel zu einer Seitenfläche und zerlegt II_t in zwei Teilkörper. Berechnen Sie das Verhältnis der Volumina.

Hinweis

Es gibt eine weitere Lösung, die den Strahlensatz verwendet (Verhältnis der beiden Höhen und der anderen Kanten ist 1:2)

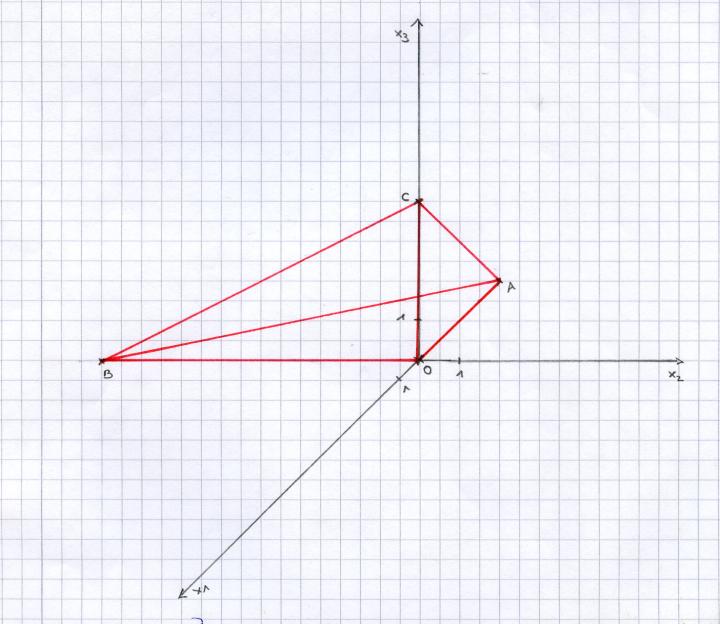
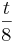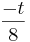d) Zeigen Sie, dass die Kugel K mit dem Mittelpunkt N_t ( $\frac{t}{8}$ | $\frac{t}{8}$ | $\frac{-t}{8}$ ) und dem Radius ρ_t = 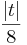$\frac{|t|}{8}$ die Inkugel der Pyramide II_t ist, also alle Begrenzungsflächen von II_t von innen berührt.

e) Die Ecken der Pyramide II_t liegen auf einer Kugel (Umkugel) mit dem Mittelpunkt M (m₁|m₂|m₃) und dem Radius r.

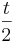Begründen Sie ohne weitere Rechnung, dass gilt: m₂ = $\frac{t}{2}$ .

Geben Sie m₁ sowie m₃ an und berechnen Sie r.

@@ Zeile 80: / Zeile 80: @@
 :{{Lösung versteckt|
 [[Bild:2 a1.jpg|800px]]
-;Bemerkung
+; Andere Lösung
- Andere Lösung bei der 2 a):
   Man hätte die Achsengeraden aufstellen können, mit dem Ursprung als Aufpunkt
   und dem jeweiligen  Richtungsvektor und dann den jeweiligen allg. Geradenpunkt

2007 VI: Unterschied zwischen den Versionen

Version vom 2. März 2010, 14:11 Uhr

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Hilfen

Oberstufe

Studien- und Berufsorientierung am RMG

Werkzeuge