2006 V: Unterschied zwischen den Versionen
| Zeile 77: | Zeile 77: | ||
| − | a)Bestimmen Sie die Koordinaten von M<sub>1</sub> und M<sub>2</sub> . (Der Punkt mit ausschließlich ganzzahligen Koordinaten wird mit M<sub>1</sub> bezeichnet.) | + | a) Bestimmen Sie die Koordinaten von M<sub>1</sub> und M<sub>2</sub> . (Der Punkt mit ausschließlich ganzzahligen Koordinaten wird mit M<sub>1</sub> bezeichnet.) |
| + | |||
[Teilergebnis: (2/5/-6)] | [Teilergebnis: (2/5/-6)] | ||
| Zeile 106: | Zeile 107: | ||
d) Zeigen Sie, dass die Punkte A (-1/0/-2) und C (-1/1/-1) auf der Kugel K<sub>1</sub> um M<sub>1</sub> liegen und bestimmen Sie die Koordinaten von B so, dass die Strecke [AB] ein Durchmesser von K<sub>1</sub> ist. | d) Zeigen Sie, dass die Punkte A (-1/0/-2) und C (-1/1/-1) auf der Kugel K<sub>1</sub> um M<sub>1</sub> liegen und bestimmen Sie die Koordinaten von B so, dass die Strecke [AB] ein Durchmesser von K<sub>1</sub> ist. | ||
| + | |||
[Teilergebnis: B (5/10/-10)] | [Teilergebnis: B (5/10/-10)] | ||
| Zeile 117: | Zeile 119: | ||
e) Das Dreieck ABC ist die Grundfläche einer Pyramide ABCD, deren Spitze D ebenfalls auf der Kugel K<sub>1</sub> liegt. Alle Punkte D, für die die Pyramiden ABCD das Volumen 11 haben, bilden zwei Kreise auf der Kugelfläche (Nachweis nicht erforderlich). | e) Das Dreieck ABC ist die Grundfläche einer Pyramide ABCD, deren Spitze D ebenfalls auf der Kugel K<sub>1</sub> liegt. Alle Punkte D, für die die Pyramiden ABCD das Volumen 11 haben, bilden zwei Kreise auf der Kugelfläche (Nachweis nicht erforderlich). | ||
Berechnen Sie zuerst die Höhe h dieser Pyramiden und anschließend mit Hilfe einer geeigneten Skizze den Radius R der beiden oben definierten Kreise. | Berechnen Sie zuerst die Höhe h dieser Pyramiden und anschließend mit Hilfe einer geeigneten Skizze den Radius R der beiden oben definierten Kreise. | ||
| + | |||
[Zur Kontrolle: h = <math>\sqrt{11}</math>] | [Zur Kontrolle: h = <math>\sqrt{11}</math>] | ||
Version vom 25. Februar 2010, 14:43 Uhr
|
|
In einem kartesischen Koordinatensystem des
3 BE
.
4 BE
.
[ Teilergebnis: S = (2/ 5 BE
.
5 BE
.
Fehler beim Parsen(Syntaxfehler): \left( -k |
 3 ist die
Ebene E: x2 - x3 - 1 = 0 , die Geradenschar gk :
3 ist die
Ebene E: x2 - x3 - 1 = 0 , die Geradenschar gk : 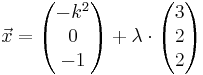 und die Gerade h :
und die Gerade h : 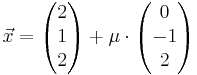 gegeben, wobei k,
gegeben, wobei k, 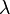 und
und 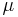 aus
aus  /
/ ) ]
) ]
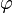 zwischen hE und h in Grad auf eine Nachkommastelle gerundet.
zwischen hE und h in Grad auf eine Nachkommastelle gerundet.
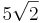 , deren Mittelpunkte M1 und M2 auf der Gerade h liegen.
, deren Mittelpunkte M1 und M2 auf der Gerade h liegen.
 K1 und Q
K1 und Q 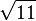 ]
]

