2008 II: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
| Zeile 4: | Zeile 4: | ||
== Aufgabe 1 == | == Aufgabe 1 == | ||
| + | Gegeben ist die Funktion | ||
| + | <math>f(x)=e^1-0,5x²</math> mit Definitionsbereich Df = IR . | ||
| + | Die Abbildung auf der folgenden Seite zeigt den Graphen G<sub>f</sub> von f. | ||
| − | < | + | a)Untersuchen Sie G<sub>f</sub> rechnerisch auf Symmetrie und Schnittpunkte mit |
| + | den Achsen. Bestimmen Sie das Verhalten von f für x → +∞ und | ||
| + | x → −∞. | ||
| + | |||
| + | b)Zeigen Sie, dass gilt: | ||
| + | f ''(x) = (x2 −1) ⋅ e1−0,5x2 . | ||
| + | Bestimmen Sie durch Rechnung das Monotonieverhalten von f und die | ||
| + | Koordinaten der Wendepunkte. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Version vom 3. Februar 2010, 08:49 Uhr
Aufgabe 1
Gegeben ist die Funktion
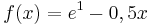 mit Definitionsbereich Df = IR .
Die Abbildung auf der folgenden Seite zeigt den Graphen Gf von f.
mit Definitionsbereich Df = IR .
Die Abbildung auf der folgenden Seite zeigt den Graphen Gf von f.
a)Untersuchen Sie Gf rechnerisch auf Symmetrie und Schnittpunkte mit den Achsen. Bestimmen Sie das Verhalten von f für x → +∞ und x → −∞.
b)Zeigen Sie, dass gilt: f (x) = (x2 −1) ⋅ e1−0,5x2 . Bestimmen Sie durch Rechnung das Monotonieverhalten von f und die Koordinaten der Wendepunkte.

