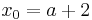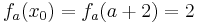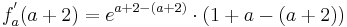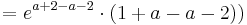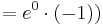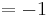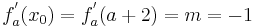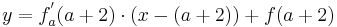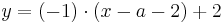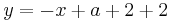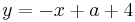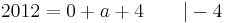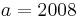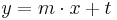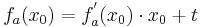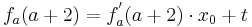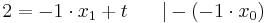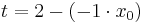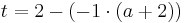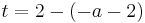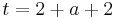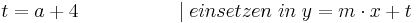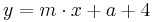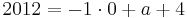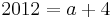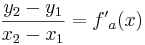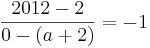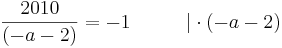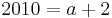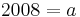Lösung von Teilaufgabe c) 1.: Unterschied zwischen den Versionen
(→Lösung; Tangentengleichung) |
(→Lösung; Tangentengleichung) |
||
| Zeile 23: | Zeile 23: | ||
=== Lösung; Tangentengleichung === | === Lösung; Tangentengleichung === | ||
| − | Die Lösung mit Hilfe der Tangentengleichen, ist der Lösungsweg, den ich | + | Die Lösung mit Hilfe der Tangentengleichen, ist der Lösungsweg, den ich bevorzuge, da es einem die Überlegung, wie eine Tangente aufgebaut ist, ersparrt.<br /> Man schlägt einfach die Tangentengleichung in seiner Formelsammlung(Mathematische Formeln und Definitionen von Barth, Mühlbauer, Nikol, Wörle) auf Seite 58 nach und setzt in diese die gegebenen Werte ein.<br />Nun muss man nur noch nach a auflösen und bekommt das Ergenis. <br /> |
Version vom 26. Januar 2010, 17:51 Uhr
Inhaltsverzeichnis |
Tangente im Punkt Wa( a + 2 / 2 ) an Gfa mit dem Schnittpunkt A (0 / 2012 )
Wichtig für diese Aufgabe ist, dass man aus den gegebenen Größen, die richtigen Schlussfolgerungen zieht:
Egal für welchen Lösungsweg man sich entscheidet, die Steigung am Punkt Wa( a + 2 / 2 ) wird in jedem Fall benötigt. Um diese zu erhalten, braucht man nur die x-Koordinaten des Punktes in die erste Ableitung einsetzen.
Lösung; Tangentengleichung
Die Lösung mit Hilfe der Tangentengleichen, ist der Lösungsweg, den ich bevorzuge, da es einem die Überlegung, wie eine Tangente aufgebaut ist, ersparrt.
Man schlägt einfach die Tangentengleichung in seiner Formelsammlung(Mathematische Formeln und Definitionen von Barth, Mühlbauer, Nikol, Wörle) auf Seite 58 nach und setzt in diese die gegebenen Werte ein.
Nun muss man nur noch nach a auflösen und bekommt das Ergenis.
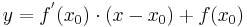
Lösung; Fußweg
Lösung; Clever
Verdeutlichung durch Grafiken
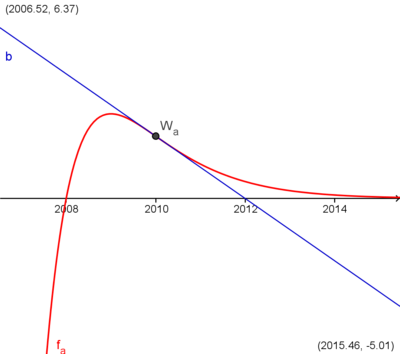
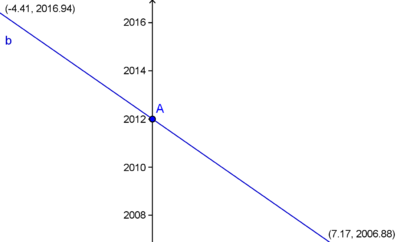
Zuerst, das Bild, auf dem sowohl die Tangente an den Wendepunkt des Graphens 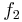 als auch der Schnittpunkt mit der y-Achse bei 2012 zu sehen ist.
als auch der Schnittpunkt mit der y-Achse bei 2012 zu sehen ist.
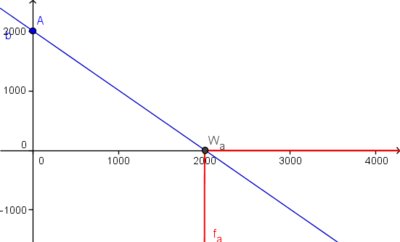
Als zweites Bild zunächst einen Zoom auf den Schnittpunkt mit der y-Achse,
 und als drittes Bild ein Zoom auf den Graphen von
und als drittes Bild ein Zoom auf den Graphen von 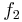 .
.