LK Mathematik Abitur NRW 2007: Unterschied zwischen den Versionen
Aus RMG-Wiki
K |
(Quelle auf Angabenseite eingefügt) |
||
| Zeile 1: | Zeile 1: | ||
| − | == | + | ==Anwendungsaufgabe zu einer Potenzfunktion== |
[[Bild:Eilif_Peterssen-_Sevilosen.jpg|250px|right]] | [[Bild:Eilif_Peterssen-_Sevilosen.jpg|250px|right]] | ||
| − | + | '''Aufgabenstellung:''' | |
| − | + | Um die Wasserstände eines Flusses vorherzusagen, kann man versuchen, die Durchflussgeschwindigkeit | |
| + | des Wassers an einer bestimmten Stelle des Flusses mit Hilfe geeigneter | ||
| + | Funktionen zu beschreiben. | ||
| + | Solche näherungsweise Beschreibungen der Durchflussgeschwindigkeiten seien z. B. gegeben | ||
| + | durch die Funktionenschar <math>f_a (t) = \frac{1}{4}t^3 - a t^2 + a^2 t</math>, mit a > 0 . | ||
| + | |||
| + | Dabei gibt <math>f_a (t)</math> die Durchflussgeschwindigkeit in <math>10^6 \frac{m^3}{Monat}</math> (Millionen Kubikmeter pro | ||
| + | Monat) und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage <math>t = 0</math> an. | ||
| + | Die Funktionen <math>f_a</math> berücksichtigen, dass es sich um einen Fluss handelt, der zeitweise | ||
| + | austrocknet.<ref>[http://www.standardsicherung.nrw.de/abitur-gost/getfile.php?file=910 Angabe als pdf Datei]</ref> | ||
==Aufgaben zur Wasserstandsaufgabe== | ==Aufgaben zur Wasserstandsaufgabe== | ||
| Zeile 19: | Zeile 28: | ||
:*[[Facharbeit Neutert/Flächengleichheit|Volumengleicheit zweier verschiedener Funktionen bis zum Zeitpunkt t<sub>0</sub>]] | :*[[Facharbeit Neutert/Flächengleichheit|Volumengleicheit zweier verschiedener Funktionen bis zum Zeitpunkt t<sub>0</sub>]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <references/> | ||
Version vom 27. Januar 2010, 13:57 Uhr
Anwendungsaufgabe zu einer Potenzfunktion
Aufgabenstellung:
Um die Wasserstände eines Flusses vorherzusagen, kann man versuchen, die Durchflussgeschwindigkeit
des Wassers an einer bestimmten Stelle des Flusses mit Hilfe geeigneter
Funktionen zu beschreiben.
Solche näherungsweise Beschreibungen der Durchflussgeschwindigkeiten seien z. B. gegeben
durch die Funktionenschar 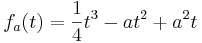 , mit a > 0 .
, mit a > 0 .
Dabei gibt 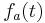 die Durchflussgeschwindigkeit in
die Durchflussgeschwindigkeit in 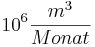 (Millionen Kubikmeter pro
Monat) und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage
(Millionen Kubikmeter pro
Monat) und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage 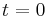 an.
Die Funktionen
an.
Die Funktionen 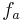 berücksichtigen, dass es sich um einen Fluss handelt, der zeitweise
austrocknet.[1]
berücksichtigen, dass es sich um einen Fluss handelt, der zeitweise
austrocknet.[1]
Aufgaben zur Wasserstandsaufgabe

