LK Mathematik Abitur NRW 2007: Unterschied zwischen den Versionen
Aus RMG-Wiki
K |
K |
||
| Zeile 2: | Zeile 2: | ||
[[Bild:Eilif_Peterssen-_Sevilosen.jpg|250px|right]] | [[Bild:Eilif_Peterssen-_Sevilosen.jpg|250px|right]] | ||
| − | Mit Hilfe der folgenden Funktion kann man beispielsweise die Wasserstände eines Flusses | + | Mit Hilfe der folgenden Funktion kann man beispielsweise die Wasserstände eines Flusses vorhersagen. Diese Beschreibung der Durchflussgeschwindigkeit sei durch die Funktionenschar f<sub>a</sub> mit <math>f(t) = \frac{1}{4} t^3 - a t^2 + a^2 t</math>, a > 0 |
Die Funktion gibt dabei die Durchflussgeschwindigkeit in <math>10^6 \frac{m^3}{Monat}</math> und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage (t = 0) an. Die Funktion berücksichtigt, dass es sich um einen Fluss handelt, der zeitweise austrocknet. | Die Funktion gibt dabei die Durchflussgeschwindigkeit in <math>10^6 \frac{m^3}{Monat}</math> und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage (t = 0) an. Die Funktion berücksichtigt, dass es sich um einen Fluss handelt, der zeitweise austrocknet. | ||
Version vom 25. Januar 2010, 22:39 Uhr
Angabe aus einer Abituraufgabe 2007; Nordrhein-Westfalen
Mit Hilfe der folgenden Funktion kann man beispielsweise die Wasserstände eines Flusses vorhersagen. Diese Beschreibung der Durchflussgeschwindigkeit sei durch die Funktionenschar fa mit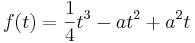 
, a > 0
Die Funktion gibt dabei die Durchflussgeschwindigkeit in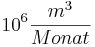 
und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage (t = 0) an. Die Funktion berücksichtigt, dass es sich um einen Fluss handelt, der zeitweise austrocknet.
