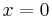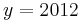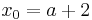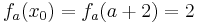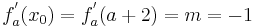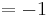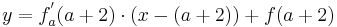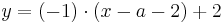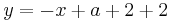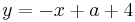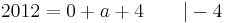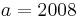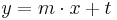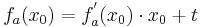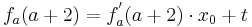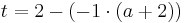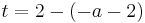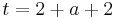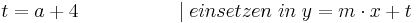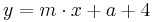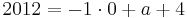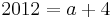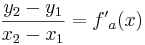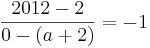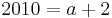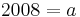Lösung von Teilaufgabe c) 1.: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: == Tangente im Punkt W<sub>a</sub>( a + 2 / 2 ) an G<sub>f<sub>a</sub></sub> mit dem Schnittpunkt A (0 / 2012 ) == <math>mit:\;</math><br /> :<math>x = 0\;</math><br...)
 
(→‎Lösung; Clever)
Zeile 59: Zeile 59:
 
:::: <math>2010 = a + 2\;</math><br />
 
:::: <math>2010 = a + 2\;</math><br />
 
:::: <math>2008 = a\;</math><br />
 
:::: <math>2008 = a\;</math><br />
 +
 +
 +
 +
 +
 +
<ggb_applet width="615" height="464"  version="3.2" ggbBase64="UEsDBBQACAAIAAEOODwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVZLc9s2ED43vwLDk93UEvgQJc1IzsTpJTNuclCaQw/tgORKQk0CLAHalH99Fw9Sr7hxks74IBHYXS722/12icWbrirJPTSKS7EMwhENCIhcFlxslkGr11ez4M31q8UG5AayhpG1bCqml0E8igIjb/n1q58WaisfCCutyWcOD8tANy0ERNUNsEJtAbQTr1mpUM7ajpecNbuP2d+Qa7VXOB/vRd3q3kleFbdc9duxPa8uuf6V3/MCGlLKfBmkE4wcV5+h0Txn5TJIqJNECCtOj5Qoio12Kxv+KIU25nvna5QQovgj4JuRkS3GFucC2rzkBWfCgLFxoBEhD7zQWzxwGqNL4JstxpqkkfOWS9kUq53SUJHuD2ikCWcyStMwoXEazWLcYXQ7p4qTaDSlM5qm84im8wQ1CgPGSOgIxfPZfD5N6CxOpskkwbf2yvkkTuPpPEqiJJ2i3p0O9yvQGoupCOtA9SndNLwYcm4279WNLPeiWnKh37Fat40lQuxFK72zxwWkMTDfik0JXhZhobaQ32WyW7nUxc71p11tX7HxZJt3spQNafCFyQQN/DNzT2tjAh2sqLWh1sL7ME4HfTiPrIV9Zu5prUouXGgeeNijDml/DFfECNC54W+fm5JlgHwISCu4vu03yJs7jzR09h/aKsO+OWTO4DL8n1wuxieUW9xBI6B0xBJY2Fa2itwbArvS2TgKyHmFW6fwCWGmWL9jAE5awKaBPm7XdS5dVksPyXsiXoz7IEwMCmPNNU4PxKMNFtPdGjvLrAqmjcS0TgkVYF9pywbRVtDwfMgMC8xpeETrD4oonY18EHa4SDsoBoL69/apR/0TnMGZUm+Z6ZHQM4PtcGocwrTefpOFP9zbqdKOl4oLGw81s7FindmEdsMyJctWwyrHTIpbmTNtp6grup8KoXuxMyPHLHbLYGIXa97BvuO+PIr2JNZbZIsApWyn6cOeYgKLbSuAQ6Z2QHHyAjgi9rakRuC2mwemIL1cWb5aIDgr0GgazqKZ+SWTOU0mL1srm0wnOWjH/itzrHgatZ1xQ8BvgzNER+38dUB2tA2Q6DMh/XBZfd8qQ7qec8jZyCwf3UfeWrmRbj5h9tz4LDkdfr6VuRn0kNd/MbwfdLVdXXSXZEkuOnJF2CX5mcCfF4y8JngMSrrLgIzPErxuhZ0VwaHDJ4kenxD9R0pBv78Qz4jtv7N243PWp+cX83cZHJPuPFnHbLx5WTbuGdVPP0Oqb2VULquKiYIIViHAW0ysRcXNdY8wanqOsNCAdUha3Ssy58o7OMuVqdGQiuxpSp3Ozhei1Jez6ZeY0KuEJkkY7f0+Bwv8I5yNcpcKXuEtOef6tAjjw6+2vdz6y/31v1BLBwgfZP3KAAQAAA4MAABQSwECFAAUAAgACAABDjg8H2T9ygAEAAAODAAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAADoEAAAAAA==" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" />

Version vom 24. Januar 2010, 01:48 Uhr

Inhaltsverzeichnis

Tangente im Punkt Wa( a + 2 / 2 ) an Gfa mit dem Schnittpunkt A (0 / 2012 )

mit:\;

x = 0\;
y = 2012\;
x_0 = a + 2\;
f_a( x_0 ) = f_a( a + 2 ) = 2\;
f^{'}_a( x_0 ) = f^{'}_a( a + 2 ) = m = -1\;


f^{'}_a( a + 2 ) = e^{a + 2 - ( a + 2 )}\cdot ( 1 + a - ( a + 2 ) )
= e^{a + 2 - a - 2 }\cdot ( 1 + a - a - 2 ) )
= e^{0}\cdot ( -1 ) )
= -1\;


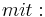
Lösung; Tangentengleichung

Tangentengleichung: siehe Formelsammlung Seite 58

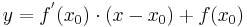
y = f^{'}( x_0 )\cdot ( x - x_0 ) + f ( x_0)


y = f^{'}_a( a + 2 )\cdot ( x - ( a + 2 )) + f ( a + 2 )
y = (-1)\cdot ( x - a - 2 ) + 2
y = -x + a + 2 + 2\;
y = -x + a + 4\;
2012 = 0 + a + 4\;\;\;\;\;\;\; | -4
a = 2008\;

Lösung; Fußweg

y = m\cdot x + t
f_a( x_0 ) = f^{'}_a( x_0 )\cdot x_0 + t
f_a( a + 2 ) = f^{'}_a( a + 2 )\cdot x_0 + t
2 = -1\cdot x_1 + t \;\;\;\;\;\; | - ( -1\cdot x_0)
t = 2 - ( -1\cdot x_0 )
t = 2 - ( -1\cdot ( a + 2 ))
t = 2 - ( -a - 2)\;
t = 2 + a + 2 \;
t = a + 4 \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; |\;einsetzen\; in\; y = m\cdot x + t


y = m\cdot x + a + 4
2012 = -1\cdot 0 + a + 4
2012 = a + 4 \;
a = 2008\;

Lösung; Clever

\frac{y_2 - y_1}{x_2 - x_1} = f{'}_a ( x )
\frac{2012 - 2}{0 - ( a + 2 )} = -1
\frac{2010}{(-a - 2 )} = -1 \;\;\;\;\;\;\;\;\;\;| \cdot( -a - 2 )
2010 = a + 2\;
2008 = a\;



Von „http://rmg.zum.de/index.php?title=Facharbeit_Andre_Etzel/Teilaufgabe_c/Lösung_von_Teilaufgabe_c)_1.&oldid=27810“