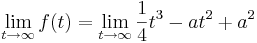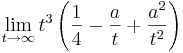Theoretische Überlegungen: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 32: | Zeile 32: | ||
:Um nun bei einer Potenzfunktion den Grenzwert zu ermitteln, | :Um nun bei einer Potenzfunktion den Grenzwert zu ermitteln, | ||
:* klammert man die höchste Potenz aus, | :* klammert man die höchste Potenz aus, | ||
| − | :* erhält ein Produkt und kann somit leichter | + | :* erhält ein Produkt und kann somit leichter als bei einer Summe, den Grenzwert bestimmen. |
| − | ::''<span style="color: darkblue">Bestimme das Verhalten von f<sub>a</sub> für <math>t \rightarrow \infty</math> | + | ::''<span style="color: darkblue">Bestimme das Verhalten von f<sub>a</sub> für <math>t \rightarrow \infty</math>.</span>'' |
::{{Lösung versteckt|1= | ::{{Lösung versteckt|1= | ||
::<math>\lim_{t\to\infty} f (t) = \lim_{t\to\infty} \frac{1}{4} t^3 - a t^2 + a^2</math> | ::<math>\lim_{t\to\infty} f (t) = \lim_{t\to\infty} \frac{1}{4} t^3 - a t^2 + a^2</math> | ||
| − | ::<math>\lim_{t\to\infty} t^3 \left( \frac{1}{4} - \frac{a}{t} + \frac{a^2}{t^2} \right)</math> | + | ::<math>\lim_{t\to\infty} t^3 \left( \frac{1}{4} - \frac{a}{t} + \frac{a^2}{t^2} \right)</math> |
| − | ::<math> | + | ::<math>t^3 \rightarrow + \infty</math> Die Klammer geht gegen <math> \frac{1}{4} \Rightarrow + \infty </math> |
::<u>Für</u><math> t\to\infty</math><u>geht die Funktion gegen</u> + <math> \infty</math> | ::<u>Für</u><math> t\to\infty</math><u>geht die Funktion gegen</u> + <math> \infty</math> | ||
| Zeile 57: | Zeile 57: | ||
::dass sie '''immer stärker ansteigt'''. (<span style="color: blue">blaue Parabelfunktion</span>) | ::dass sie '''immer stärker ansteigt'''. (<span style="color: blue">blaue Parabelfunktion</span>) | ||
| − | ::Wenn man nun | + | ::Wenn man nun anhand der Funktion vorhersagen soll, wieviel Wasser in zwei Jahren ( also 24 Monaten ) durch den Fluss fließt, '''ergibt sich ein Wasserstandswert, der mit sehr hoher Wahrscheinlichkeit nicht erreicht werden wird'''. |
::Je größer t wird, desto unwahrscheinlicher wird die Durchflussgeschwindigkeit, die sich errechnen lässt. | ::Je größer t wird, desto unwahrscheinlicher wird die Durchflussgeschwindigkeit, die sich errechnen lässt. | ||
Version vom 25. Januar 2010, 23:10 Uhr
Theoretische Fragen zur Wasserstandsaufgabe
Warum liegt kein Punkt der Funktionsgraphen von fa im Bereich 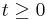 unterhalb der t - Achse und inwiefern ist dies mit dem zugrunde liegenden Sachverhalt vereinbar.
unterhalb der t - Achse und inwiefern ist dies mit dem zugrunde liegenden Sachverhalt vereinbar.
|
|
Es soll nun das Verhalten von fa für 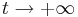 angegeben werden und begründet werden, ob die Funktionen auch nach den ersten acht Monaten noch eine sinnvolle Beschreibung der Durchflussgeschwindigkeit liefern.
angegeben werden und begründet werden, ob die Funktionen auch nach den ersten acht Monaten noch eine sinnvolle Beschreibung der Durchflussgeschwindigkeit liefern.
- Um das Verhalten eines Graphen, welcher gegen
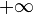 geht, zu bestimmen, wird statt f (t)
geht, zu bestimmen, wird statt f (t) 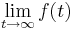 geschrieben.
geschrieben.
- Um nun bei einer Potenzfunktion den Grenzwert zu ermitteln,
- klammert man die höchste Potenz aus,
- erhält ein Produkt und kann somit leichter als bei einer Summe, den Grenzwert bestimmen.
- Bestimme das Verhalten von fa für
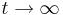 .
.
- Bestimme das Verhalten von fa für
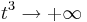 Die Klammer geht gegen
Die Klammer geht gegen 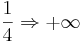
- Für
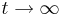 geht die Funktion gegen +
geht die Funktion gegen + 
- Für
|
Funktion f (t), Ableitung f '(t) |
Hier geht's zur Aufgabe: Berechnung des Wasservolumens in den ersten sechs Monaten
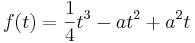 ist in diesem Quadranten kein Punkt definiert.
ist in diesem Quadranten kein Punkt definiert.