Integralberechnung: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: ===Aufgabe: Flächenberechnung einer Funktion=== '''''<span style="color: darkorange">Ermittle für a = 3, wie viel Liter Wasser in den ersten sechs Monaten durch den F...) |
|||
| Zeile 41: | Zeile 41: | ||
}} | }} | ||
| − | [[Facharbeit Neutert/Flächengleichheit|Flächengleichheit zweier verschiedener Funktionen]] | + | |
| + | [[Facharbeit Neutert/Flächengleichheit|Hier geht's zur Aufgabe: Flächengleichheit zweier verschiedener Funktionen]], | ||
| + | |||
| + | [[Facharbeit Neutert|Hier geht's zurück zur Übersicht]] | ||
Version vom 19. Januar 2010, 22:30 Uhr
Aufgabe: Flächenberechnung einer Funktion
Ermittle für a = 3, wie viel Liter Wasser in den ersten sechs Monaten durch den Fluss fließen.
|
|
- Gebe die Funktion F (t) an und errechne mit ihr für a = 3, wieviel Liter in den ersten sechs Monaten durch den Fluss geflossen sind.
- Die obere Grenze ist: 6 Nach den ersten sechs Monaten
- Die untere Grenze ist: 0
- Für a = 3 fließen in den ersten sechs Monaten 27*109 Liter Wasser durch den Fluss. ( 27*106 m3 = 27*109 Liter)
- Merke: Die Funktion muss im Intervall stetig und differenzierbar sein ! Ist dies nicht erfüllt, ist eine Integration nicht möglich.
Hier geht's zur Aufgabe: Flächengleichheit zweier verschiedener Funktionen,
![\int_{a}^{b} x^n \,dx = \left[ \frac{x^{n+1}}{n+1} \right]_{a}^{b}](/images/math/c/4/e/c4e09d0a32630fc2d68d22072dd7ccd8.png)
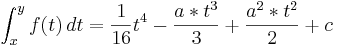
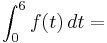
![\left[ \frac{1}{16}t^4 - \frac{3*t^3}{3} + \frac{3^2*t^2}{2}\right ]_{0}^{6} = 27 - 0 = 27](/images/math/4/9/a/49a1f445fbc0fa11cad513f8131a8bd7.png)

