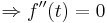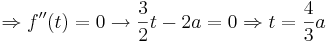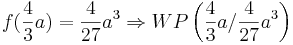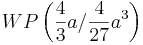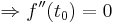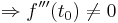Wendepunkt: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Die Seite wurde neu angelegt: ===Aufgabe: Wendepunkt=== '''''<span style="color: darkorange">Es soll, in Abhängigkeit von a bestimmt werden, wann die Druchflussgeschwindigkeit besonders stark absin...) |
|||
| Zeile 38: | Zeile 38: | ||
|} | |} | ||
| − | [[Facharbeit Neutert/Theoretische Überlegungen|Aufgabe: Theoretische Überlegungen]] | + | |
| + | [[Facharbeit Neutert/Theoretische Überlegungen|Hier geht's zur Aufgabe: Theoretische Überlegungen]] | ||
| + | |||
| + | [[Facharbeit Neutert|Hier geht's zurück zur Übersicht]] | ||
Version vom 19. Januar 2010, 22:29 Uhr
Aufgabe: Wendepunkt
Es soll, in Abhängigkeit von a bestimmt werden, wann die Druchflussgeschwindigkeit besonders stark absinkt. Dieser Wert soll zum Zeitpunkt t berechnet werden.
|
Die blaue Funktion zeigt die Ableitung f '(t) der schwarzen Funktion f (t) für a = 3. |