Übungsaufgaben: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 1: | Zeile 1: | ||
| + | {| | ||
| + | ! width="910" | | ||
| + | |- | ||
| + | | valign="top" | | ||
= <span style="color: blue">Übungsaufgaben</span> = | = <span style="color: blue">Übungsaufgaben</span> = | ||
| Zeile 108: | Zeile 112: | ||
<span style="color: blue">'''Du hast den ganzen Lernpfad durchgearbeitet!'''</span> <br /> | <span style="color: blue">'''Du hast den ganzen Lernpfad durchgearbeitet!'''</span> <br /> | ||
<span style="color: blue">'''Jetzt solltest du dich mit den Eigenschaften von Funktionen und ihrer Graphen auskennen.'''</span> <br /> <br /> | <span style="color: blue">'''Jetzt solltest du dich mit den Eigenschaften von Funktionen und ihrer Graphen auskennen.'''</span> <br /> <br /> | ||
| + | |} | ||
[[Facharbeit Florian Wilk|Zurück zur Übersicht]] | [[Facharbeit Florian Wilk|Zurück zur Übersicht]] | ||
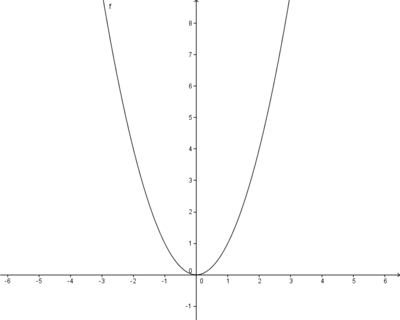
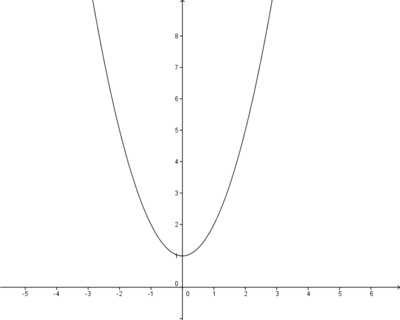
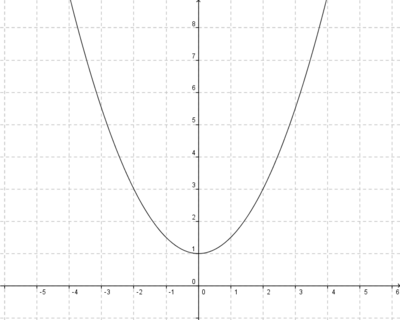
 Streckung um 0,5 in y-Richtung
Streckung um 0,5 in y-Richtung 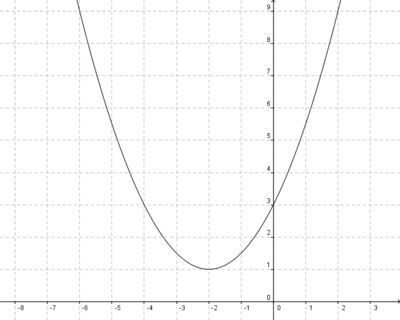
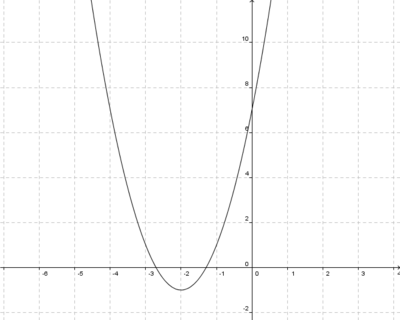
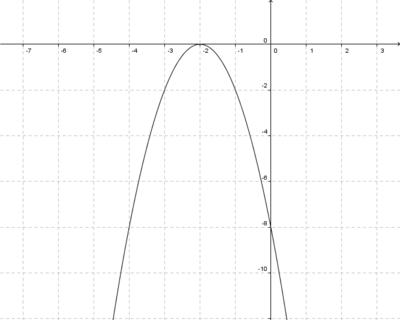
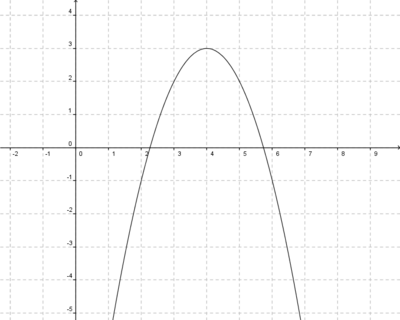

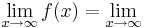 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=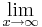 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=
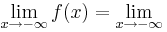 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=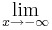 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=