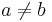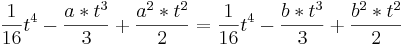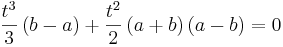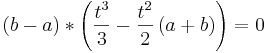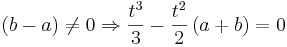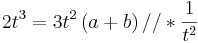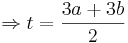LK Mathematik Abitur NRW 2007: Unterschied zwischen den Versionen
(→Aufgabe: Art der Extremwerte berechnen) |
(→Angabe) |
||
| Zeile 4: | Zeile 4: | ||
Mit Hilfe der folgenden Funktion kann man beispielsweise die Wasserstände eines Flusses vorherzusagen. Diese Beschreibung der Durchflussgeschwindigkeit sei durch die Funktionenschar f<sub>a</sub> mit <math>f(t) = \frac{1}{4} t^3 - a t^2 + a^2 t</math>, a > 0 | Mit Hilfe der folgenden Funktion kann man beispielsweise die Wasserstände eines Flusses vorherzusagen. Diese Beschreibung der Durchflussgeschwindigkeit sei durch die Funktionenschar f<sub>a</sub> mit <math>f(t) = \frac{1}{4} t^3 - a t^2 + a^2 t</math>, a > 0 | ||
| − | Die Funktion gibt dabei die Durchflussgeschwindigkeit in | + | Die Funktion gibt dabei die Durchflussgeschwindigkeit in <math>10^6 \frac{m^3}{Monat}</math> und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage (t = 0) an. Die Funktion berücksichtigt, dass es sich um einen Fluss handelt, der zeitweise austrocknet. |
| − | + | ||
| − | (t = 0) an. Die Funktion berücksichtigt, dass es sich um einen Fluss handelt, der zeitweise austrocknet. | + | |
Version vom 15. Januar 2010, 17:48 Uhr
Inhaltsverzeichnis |
Angabe
Mit Hilfe der folgenden Funktion kann man beispielsweise die Wasserstände eines Flusses vorherzusagen. Diese Beschreibung der Durchflussgeschwindigkeit sei durch die Funktionenschar fa mit 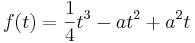 , a > 0
, a > 0
Die Funktion gibt dabei die Durchflussgeschwindigkeit in 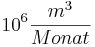 und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage (t = 0) an. Die Funktion berücksichtigt, dass es sich um einen Fluss handelt, der zeitweise austrocknet.
und t die verstrichene Zeit in Monaten seit Beginn der Vorhersage (t = 0) an. Die Funktion berücksichtigt, dass es sich um einen Fluss handelt, der zeitweise austrocknet.
Aufgabe: Nullstellen
Es soll bestimmt werden, abhängig vom Parameter a, zu welchen Monaten kein Wasser durch den Fluss fließt.
|
|
Aufgabe: Extremwerte
Es soll, in Abhängigkeit von a, ermittelt werden, zu welchen Zeitpunkten t ein relatives Maximum bzw. Minimum vorliegt. Diese Funktionswerte sollen berechnet werden.
Aufgabe: Extremwerte berechnen
|
Maxima und Minima sind Punkte auf einer Funktion, die in ihrem im Umkreis die höchsten beziehungsweise tiefsten Punkte auf dem Graphen sind. Um diese Extremwerte einer Funktion zu errechnen, wird die erste Ableitung benötigt.
|
|
Aufgabe: Art der Extremwerte berechnen
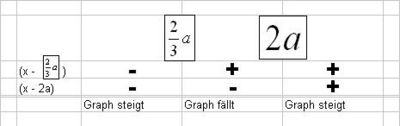
Man hat nun die Extremwerte in Abhängigkeit von a ermittelt. Um nun zu prüfen ob es sich bei den Extrema um Maxima oder Minima handelt, kann man hier anhand verschiedener Lösungen vorgehen.
|
|
- Lösung 3: Vorzeichentabelle
|
|
Aufgabe: Wendepunkt
Es soll, in Abhängigkeit von a bestimmt werden, wann die Druchflussgeschwindigkeit besonders stark absinkt. Dieser Wert soll zum Zeitpunkt t berechnet werden.
|
Die blaue Funktion zeigt die Ableitung f '(t) der schwarzen Funktion f (t). |
Aufgabe: Theoretische Überlegungen zur Funktion
Warum liegt kein Punkt der Funktionsgraphen von fa im Bereich 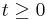 unterhalb der t - Achse und inwiefern ist dies mit dem zugrunde liegenden Sachverhalt vereinbar.
unterhalb der t - Achse und inwiefern ist dies mit dem zugrunde liegenden Sachverhalt vereinbar.
- Begründe dies.
- Es liegt kein Punkt im Intervall
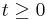 unterhalb der t - Achse, da es hier um eine Funktion mit realem Bezug geht. Läge ein Punkt bei der gegebenen Aufgabenstellung im vierten Quadranten, würde dies bedeuten, dass eine negative Durchflussgeschwindigkeit vorliegt. Dies ist nicht möglich, da sonst ein negatives Volumen an Wasser im Fluss vorhanden wäre. Deshalb ist kein Punkt der Funktionsgraphen fa im vierten Quadranten definiert.
unterhalb der t - Achse, da es hier um eine Funktion mit realem Bezug geht. Läge ein Punkt bei der gegebenen Aufgabenstellung im vierten Quadranten, würde dies bedeuten, dass eine negative Durchflussgeschwindigkeit vorliegt. Dies ist nicht möglich, da sonst ein negatives Volumen an Wasser im Fluss vorhanden wäre. Deshalb ist kein Punkt der Funktionsgraphen fa im vierten Quadranten definiert.
- Es liegt kein Punkt im Intervall
- Um das Verhalten eines Graphen, welcher gegen
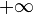 geht, zu bestimmen, wird statt f (t)
geht, zu bestimmen, wird statt f (t) 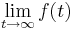 geschrieben. Um nun bei einer Potenzfunktion den Grenzwert zu ermitteln, klammert man die höchste Potenz aus, erhält ein Produkt und kann somit leichter, als bei einer Summe, den Grenzwert bestimmen.
geschrieben. Um nun bei einer Potenzfunktion den Grenzwert zu ermitteln, klammert man die höchste Potenz aus, erhält ein Produkt und kann somit leichter, als bei einer Summe, den Grenzwert bestimmen.
- Bestimme das Verhalten von fa für
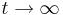 angegeben werden.
angegeben werden.
- Bestimme das Verhalten von fa für
- Für
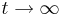 geht die Funktion gegen +
geht die Funktion gegen + 
- Für
- Des Weiteren soll begründet werden, ob die Funktionen auch nach den ersten 8 Monate noch eine sinnvolle Beschreibung der Durchflussgeschwindigkeit liefern, aufgrund des berechneten Grenzwertes in der vorherigen Aufgabe.
- Nach den ersten 8 Monaten verhält sich die Funktion so, dass sie immer stärker ansteigt. Dies ist an der Parabel, welche die Steigung anzeigt, erkennbar. Da die Funktion fa (t) vorhersagen soll, wieviel Wasser sich zu einem Zeitpunkt t im Wasser befindet. Wenn man nun, anhand der Funktion vorhersagen soll, wieviel Wasser in zwei Jahren ( also 24 Monaten ) ergibt sich ein Wasserstandswert, der mit sehr hoher Wahrscheinlichkeit nicht erreicht werden wird.
- Nehmen wir nun mal das Beispiel t = 24 und a = 3.
- Da das Ergebnis in Millionenkubikmeter pro Monat angegeben ist, wäre dann der Wert
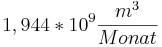 . Dieser Wasserstandswert wäre eine ziemlich grobe Abweichung vom Realwert. Aus diesem Grund handelt es sich bei der Funktion eher um eine Sinusähnliche Funktion, als um eine, die gen Unendlich exponential ansteigt. Dies würde heißen, dass das zweite Austrocknen auf der t - Achse verschoben wird, wieder als t = 0 definiert werden würde, und die Funktion fa (t) wieder von vorne starten würde.
. Dieser Wasserstandswert wäre eine ziemlich grobe Abweichung vom Realwert. Aus diesem Grund handelt es sich bei der Funktion eher um eine Sinusähnliche Funktion, als um eine, die gen Unendlich exponential ansteigt. Dies würde heißen, dass das zweite Austrocknen auf der t - Achse verschoben wird, wieder als t = 0 definiert werden würde, und die Funktion fa (t) wieder von vorne starten würde.
- Da das Ergebnis in Millionenkubikmeter pro Monat angegeben ist, wäre dann der Wert
Aufgabe: Flächenberechnung einer Funktion
Ermittle für a = 3, wie viel Liter Wasser in den ersten sechs Monaten durch den Fluss fließen.
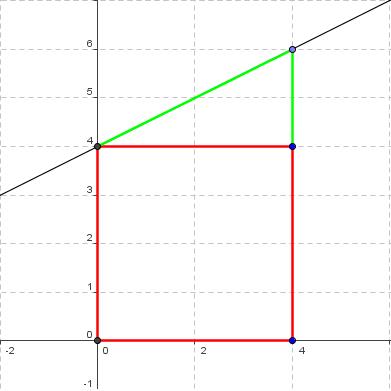
- Um Auszurechnen, wieviel Kubikliter Wasser durch den Fluss fließen, errechnet man die Fläche unter der Funktion. Einfache, bereits bekannte Flächenberechnungen gibt es bei linearen Funktionen. Um hier die Fläche auszurechnen, die der Graph mit der x - Achse einschließt, nimmt man einfach die gebräuchlichen Flächenformeln, wie die Rechtecksformel oder die Dreiecksformel.
- Hier siehst du ein Beispiel dazu.
- Bei Funktionen mit höcheren Potenzen benötigt man die Hilfe der Integralrechnung.
- Es muss gelten: F' (t) = f (t)
|
- a ist die untere Grenze, b die obere. Die Funktion wird im Intervall [ a; b ] integriert.
- Gebe die Funktion F (t) an und errechne mit ihr für a = 3, wieviel Liter in den ersten sechs Monaten durch den Fluss geflossen sind.
- Die obere Grenze ist: 6 Nach den ersten sechs Monaten
- Die untere Grenze ist: 0
- Für a = 3 fließen in den ersten sechs Monaten 27*109 Liter Wasser durch den Fluss. ( 27*106 m3 = 27*109 Liter)
- Merke: Die Funktion muss im Intervall stetig und differenzierbar sein ! Ist dies nicht erfüllt, ist eine Integration nicht möglich.
Aufgabe: Flächengleichheit zweier Funktionen
Betrachte nun zwei unterschiedliche Funktionen fa1 und fa2. Es soll der Zeitpunkt bestimmt werden, zu dem für beide Funktionsannahmen (seit t = 0) genau gleich viel Wasser durch den Fluss geflossen wäre.
|
|
- Im Weiteren wird eine Funktion mit Parameter a, die andere mit Parameter b bezeichnet. Wobei gilt:
- Fa (t) = Fb (t)
- Somit sind zwei Funktionen Fa und Fb flächenmäßig gleich groß, wenn für frei wählbares a und b gilt, dass sie bis
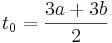 integriert werden. Bei t0 handelt es sich um die obere Integrationsgrenze.
integriert werden. Bei t0 handelt es sich um die obere Integrationsgrenze.
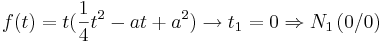
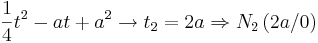
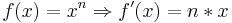 n-1
n-1
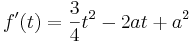
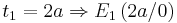
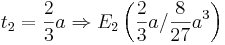
 Rechtskrümmung bzw Rechtskurve
Rechtskrümmung bzw Rechtskurve
 relatives Maximum
relatives Maximum
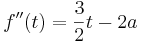
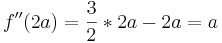
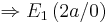 ist Minimum
ist Minimum
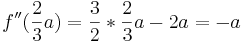
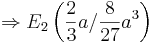 ist Maximum
ist Maximum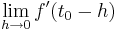
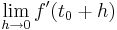 ein.
ein.
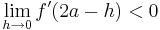 und
und 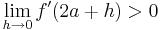
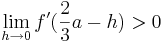 und
und 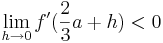
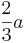 der Graph steigt.
der Graph steigt.
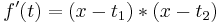 ,
,
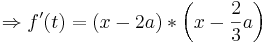
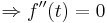
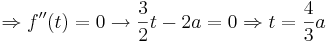
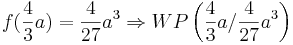
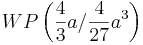
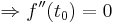
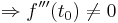
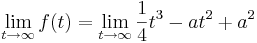
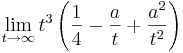
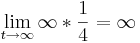
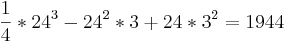
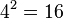
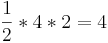
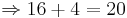
![\Rightarrow \int_{0}^{4} f (x)\,dx = \int_{0}^{4} \frac{1}{2}x + 4 \,dx = \left[ \frac{x^2}{4} + 4x \right]_{0}^{4}](/images/math/8/0/5/8058fe8c427bbc24d407f017e0f4b047.png)
![\Rightarrow \left[ \frac{4^2}{4} + 4*4 \right] - \left[ \frac{0^2}{4} + 4*0 \right]](/images/math/8/c/8/8c8935045647fe58b43d3c98913c8d15.png)
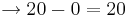
![\int_{a}^{b} x^n \,dx = \left[ \frac{x^{n+1}}{n+1} \right]_{a}^{b}](/images/math/c/4/e/c4e09d0a32630fc2d68d22072dd7ccd8.png)
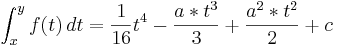
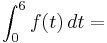
![\left[ \frac{1}{16}t^4 - \frac{3*t^3}{3} + \frac{3^2*t^2}{2}\right ]_{0}^{6} = 27 - 0 = 27](/images/math/4/9/a/49a1f445fbc0fa11cad513f8131a8bd7.png)