Symmetrie von Funktionsgraphen: Unterschied zwischen den Versionen
| Zeile 63: | Zeile 63: | ||
c) f(x)=x<sup>3</sup>-1 <br /> | c) f(x)=x<sup>3</sup>-1 <br /> | ||
| − | a) | + | a) <br /> |
:f(x)=cosx <br /> | :f(x)=cosx <br /> | ||
:f(-x)=cos-x <br /> | :f(-x)=cos-x <br /> | ||
| − | f(-x)=-cosx <br /> | + | :f(-x)=-cosx <br /> |
| − | f(-x)=-f(x) <br /> | + | :f(-x)=-f(x) <br /> |
| − | f(x)=-f(-x) <br /> | + | :f(x)=-f(-x) <br /> |
| − | → Punktsymmetrie zum Ursprung <br /> <br /> | + | ::→ Punktsymmetrie zum Ursprung <br /> <br /> |
| − | b) f(x)=x<sup>4</sup>-2x<sup>2</sup>+3 <br /> | + | b) <br /> |
| − | f(-x)=(-x)<sup>4</sup>-2(-x)<sup>2</sup>+3 <br /> | + | :f(x)=x<sup>4</sup>-2x<sup>2</sup>+3 <br /> |
| − | f(-x)=x<sup>4</sup>-2x<sup>2</sup>+3=f(x) <br /> | + | :f(-x)=(-x)<sup>4</sup>-2(-x)<sup>2</sup>+3 <br /> |
| − | → Achsensymmetrie zur y-Achse <br /> | + | :f(-x)=x<sup>4</sup>-2x<sup>2</sup>+3=f(x) <br /> |
| + | ::→ Achsensymmetrie zur y-Achse <br /> | ||
| − | c) f(x)=x<sup>3</sup>-1 <br /> | + | c) <br /> |
| − | f(-x)=-x<sup>3</sup>-1 <br /> | + | :f(x)=x<sup>3</sup>-1 <br /> |
| − | → Weder Achsensymmetrie zur y-Achse noch Punktsymmetrie zum Ursprung <br /> | + | :f(-x)=-x<sup>3</sup>-1 <br /> |
| + | ::→ Weder Achsensymmetrie zur y-Achse noch Punktsymmetrie zum Ursprung <br /> | ||
Version vom 13. Januar 2010, 18:18 Uhr
Inhaltsverzeichnis |
Symmetrie von Funktionsgraphen
Achsensymmetrie
Im untenstehenden Koordinatensystem ist der Graph der Funktion f(x)=x2+2 abgebildet. Bei der Betrachtung des Graphen fällt auf, dass man bei einer Spiegelung an der y-Achse den jeweils anderen Teil des Graphen erhält. Dies wird als Achsensymmetrie zur y-Achse bezeichnet. Zum Beweis dieser Symmetrie nutzt man den Zusammenhang f(x)=f(-x). Wenn also das Einsetzen von f(x) und f(-x) den gleichen Funktionswert ergibt, handelt es sich um einen achsensymmetrischen Graphen.
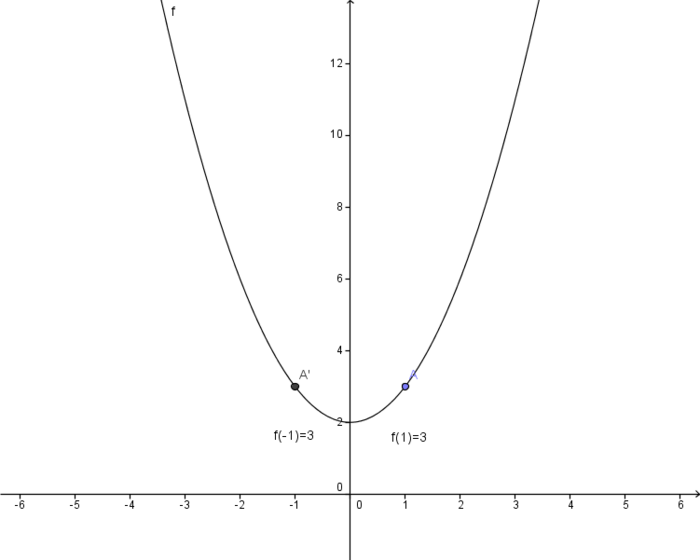 Setzt man beispielsweise in diesem Fall 1 und -1 in den Funktionsterm ein, so kommt beide Male das gleiche Ergebnis dabei heraus:
Setzt man beispielsweise in diesem Fall 1 und -1 in den Funktionsterm ein, so kommt beide Male das gleiche Ergebnis dabei heraus:
- f(1)=12+2=3
- f(-1)=(-1)2+2=3
- f(1)=12+2=3
In der Regel wird dieser Beweis allerdings allgemein durchgeführt, indem man –x in den Funktionsterm einsetzt:
- f(x)=x2+2
- f(-x)=(-x)2+2
- =x2+2
- =f(x)
- f(x)=x2+2
Punktsymmetrie zum Ursprung
Im nebenstehenden Koordinatensystem ist der Graph der Funktion f(x)=x3 dargestellt. Hier lässt sich nicht wie im vorigen Fall eine Symmetrie zu einer Achse feststellen. Stattdessen ist diese Funktion symmetrisch zum Ursprung und wird daher als Punktsymmetrie zum Ursprung bezeichnet. Hierbei gilt der Zusammenhang f(x)=-f(-x). Das bedeutet, dass die Funktionswerte von f(x) und f(-x) vom Betrag her gleich sein müssen, aber unterschiedliche Vorzeichen haben.
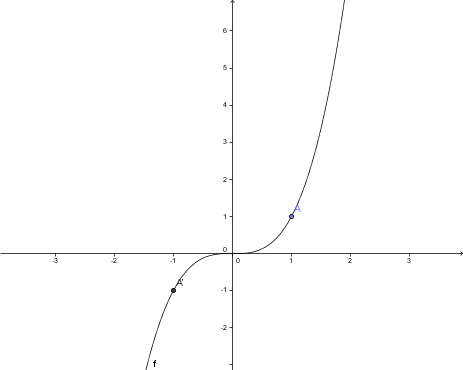 Dies lässt sich leicht durch ein Beispiel beweisen:
Dies lässt sich leicht durch ein Beispiel beweisen:
- f(1)=13=1
- f(-1)=(-1)3=-1
- f(1)=13=1
Wie auch der Beweis der Achsensymmetrie wird dieser Beweis in der Regel allgemein geführt:
- f(x)=x3
- f(-x)=(-x)3
- =-x3
- =-f(x)
- f(x)=x3
Zusammenfassung:
Achsensymmetrie zur y-Achse: f(x)=-f(x)
Punktsymmetrie zum Ursprung: f(-x)=-f(x)
Ganzrationale Funktionen
Aufgabe: Betrachte die unten abgebildeten Funktionen und untersuche sie auf Symmetrieeigenschaften. Versuche anhand der Exponenten der Funktionen Regeln für die Symmetrieeigenschaften bei ganzrationalen Funktionen aufzustellen.
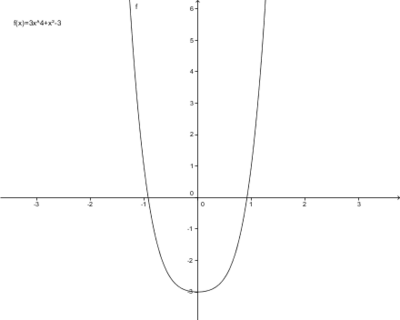
a) f(x)=3x4+x2-3
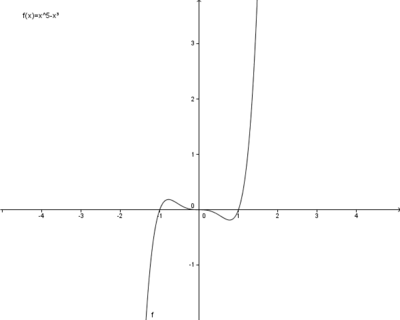
b) f(x)=x5-x3
c) f(x)=2x8-4x6+2
d) f(x)=3x7-5x5+2x3
a)
b)
c)
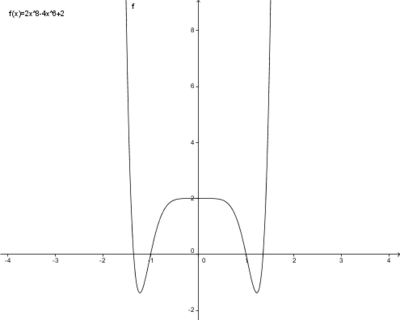
d)
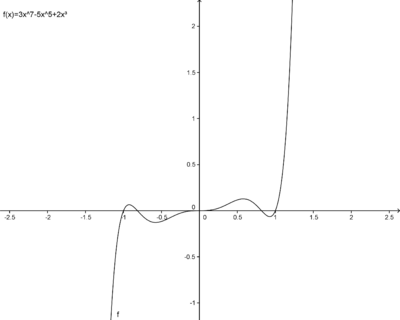
Bei den Funktionen a und c handelt es sich um achsensymmetrische Funktionen, bei b und d um punktsymmetrische Funktionen. Betrachtet man die Exponenten der Funktionen, fällt auf, dass die achsensymmetrischen Funktionen nur gerade Exponenten enthalten. Deshalb werden sie gerade Funktionen genannt (Zahlen ohne Variable x gelten als gerade). Die punktsymmetrischen Funktionen enthalten nur ungerade Exponenten und heißen daher ungerade Funktionen.
Zusammenfassung: Ganzrationale Funktionen
Eine gerade Funktion enthält nur geradzahlige Exponenten und ist achsensymmetrisch zur y-Achse.
Eine ungerade Funktion enthält nur ungeradzahlige Exponenten und ist punktsymmetrisch zum Ursprung.
Beispielaufgaben
Aufgabe 1:
Untersuche folgende Funktionen rechnerisch auf Symmetrieeigenschaften.
a) f(x)=cosx
b) f(x)=x4-2x2+3
c) f(x)=x3-1
a)
- f(x)=cosx
- f(-x)=cos-x
- f(-x)=-cosx
- f(-x)=-f(x)
- f(x)=-f(-x)
- → Punktsymmetrie zum Ursprung
- → Punktsymmetrie zum Ursprung
b)
- f(x)=x4-2x2+3
- f(-x)=(-x)4-2(-x)2+3
- f(-x)=x4-2x2+3=f(x)
- → Achsensymmetrie zur y-Achse
- → Achsensymmetrie zur y-Achse
c)
- f(x)=x3-1
- f(-x)=-x3-1
- → Weder Achsensymmetrie zur y-Achse noch Punktsymmetrie zum Ursprung
- → Weder Achsensymmetrie zur y-Achse noch Punktsymmetrie zum Ursprung

