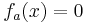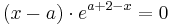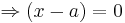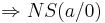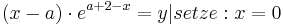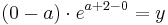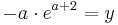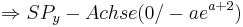Lösung: Schnittpunkte mit den Koordinatenachsen: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→2. Schnittpunkt mit der y-Achse) |
(→2. Schnittpunkt mit der y-Achse) |
||
| Zeile 28: | Zeile 28: | ||
<math>( x - a )\cdot e^{a+2-x} = y | setze: x = 0</math> <br /> | <math>( x - a )\cdot e^{a+2-x} = y | setze: x = 0</math> <br /> | ||
<math>( 0 - a )\cdot e^{a+2-0} = y</math><br /> | <math>( 0 - a )\cdot e^{a+2-0} = y</math><br /> | ||
| − | <math>-a\cdot e^{a+2} = y</math> | + | <math>-a\cdot e^{a+2} = y</math><br /> |
| + | |||
<math>\Rightarrow SP_y-Achse (0 / -a e^{a+2} )</math> | <math>\Rightarrow SP_y-Achse (0 / -a e^{a+2} )</math> | ||
Version vom 11. Januar 2010, 20:54 Uhr
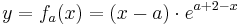 mit
mit 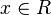 ;
; 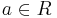
Schnittpunkte mit den Koordinatenachsen
1. Nullstellen
Da die e-Funktion ( in diesem Fall ea + 2 - x) immer streng monoton steigend und
immer positiv ist, gibt es nur für ( x - a ) = 0 Nullstellen.
x - a = 0 / +a
x = a
Für a < 0 NS ( <0 / 0 )
Für a > 0 NS ( >0 / 0 )
Für a = 0 NS ( 0 / 0 )
2. Schnittpunkt mit der y-Achse
Für a < 0 SPy-Achse( 0 / >0 )
Für a > 0 SPy-Achse( 0 / <0 )
Für a = 0 SPy-Achse( 0 / 0 )