BMT8 2008: Unterschied zwischen den Versionen
(Lösungen ergänzt) |
(Lösungen verbessert) |
||
| Zeile 141: | Zeile 141: | ||
:Am häufigsten wurden '''mangelhafte Reifen''' festgestellt. | :Am häufigsten wurden '''mangelhafte Reifen''' festgestellt. | ||
| − | :mögliche '''Begründung''' durch Größenvergleich in der | + | :mögliche '''Begründung''' durch Größenvergleich in der '''Bruch'''darstellung: |
| − | :: | + | ::*mangelhafte Beleuchtung: "Jedes 6. Fahrrad" entspricht <math>\frac{1}{6}</math> aller Fahrräder |
| − | ::15% = <math>\frac{15}{100}</math> = <math>\frac{3}{20}</math> | + | ::*mangelhafte Bremsen: 15% = <math>\frac{15}{100}</math> = <math>\frac{3}{20}</math> |
| − | :: | + | ::*mangelhafte Reifen: <math>\frac{1}{5}</math> |
| − | ::<math>\frac{1}{5}</math> > <math>\frac{1}{6}</math> | + | ::Größenvergleich der Brüche: |
| − | ::<math>\frac{1}{5}</math> = <math>\frac{4}{20}</math> > <math>\frac{3}{20}</math> | + | :::*<math>\frac{1}{5}</math> > <math>\frac{1}{6}</math> |
| + | :::*<math>\frac{1}{5}</math> = <math>\frac{4}{20}</math> > <math>\frac{3}{20}</math> | ||
::Der Bruch <math>\frac{1}{5}</math> hat den größten Wert, der zugehörigen Mangel wurde am häufigsten festgestellt. | ::Der Bruch <math>\frac{1}{5}</math> hat den größten Wert, der zugehörigen Mangel wurde am häufigsten festgestellt. | ||
| − | :mögliche '''Begründung''' durch Größenvergleich in der | + | :mögliche '''Begründung''' durch Größenvergleich in der '''Prozent'''darstellung: |
| − | ::mangelhafte Beleuchtung: <math>\frac{1}{6}</math> entspricht ca. 17% | + | ::*mangelhafte Beleuchtung: <math>\frac{1}{6}</math> entspricht ca. 17% |
| − | ::mangelhafte Bremsen: 15% | + | ::*mangelhafte Bremsen: 15% |
| − | ::mangelhafte Reifen: <math>\frac{1}{5}</math> = 20% | + | ::*mangelhafte Reifen: <math>\frac{1}{5}</math> = 20% |
}} | }} | ||
| Zeile 238: | Zeile 239: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
:[[Bild:BMT8_08_A6b_01.jpg|right]]Zeichne eine beliebige Strecke [AB] der Länge a. | :[[Bild:BMT8_08_A6b_01.jpg|right]]Zeichne eine beliebige Strecke [AB] der Länge a. | ||
| − | :Zeichne zwei Kreise mit dem Radius a und den Mittelpunkten A und B. Der Schnittpunkt der beiden Kreise ist der Eckpunkt D der Raute. | + | :[[Bild:BMT8_08_A6b_02.jpg|right]]Zeichne zwei Kreise mit dem Radius a und den Mittelpunkten A und B. Der Schnittpunkt der beiden Kreise ist der Eckpunkt D der Raute. |
| − | + | :[[Bild:BMT8_08_A6b_03.jpg|right]]Zeichne zwei Kreise mit dem Radius a und den Mittelpunkten B und D. Der Schnittpunkt der beiden Kreise ist der Eckpunkt C der Raute. | |
| − | + | ||
}} | }} | ||
| Zeile 299: | Zeile 299: | ||
:Überlegung am Zahlenstrahl: | :Überlegung am Zahlenstrahl: | ||
::[[Bild:BMT8:08_A08b.jpg]] | ::[[Bild:BMT8:08_A08b.jpg]] | ||
| − | ::<math>\frac{1}{3}</math> = <math>\frac{2}{6}</math> = <math>\frac{4}{12}</math> | + | ::Es gilt: <math>\frac{1}{3}</math> = <math>\frac{2}{6}</math> = <math>\frac{4}{12}</math> und <math>\frac{1}{2}</math> = <math>\frac{3}{6}</math> = <math>\frac{6}{12}</math> |
| − | + | ::Der Bruch <math>\frac{5}{12}</math> liegt genau in der Mitte zwischen <math>\frac{4}{12}</math> und <math>\frac{6}{12}</math> | |
| − | ::<math>\frac{5}{12}</math> liegt in der Mitte zwischen <math>\frac{4}{12}</math> und <math>\frac{6}{12}</math> | + | |
}} | }} | ||
| Zeile 321: | Zeile 320: | ||
:mögliche Lösungswege: | :mögliche Lösungswege: | ||
::l = b + <math>\frac{1}{6}</math>b = 18 cm + 3 cm = 21 cm | ::l = b + <math>\frac{1}{6}</math>b = 18 cm + 3 cm = 21 cm | ||
| − | ::l = b + <math>\frac{1}{6}</math>b = <math>\frac{7}{6}</math>b = <math>\frac{7}{6}</math>·18 cm = 21 cm | + | ::oder |
| + | ::l = b + <math>\frac{1}{6}</math>b = <math>\frac{7}{6}</math>b = <math>\frac{7}{6}</math>·18 cm = (18 cm : 6)· 7 = 21 cm | ||
}} | }} | ||
Version vom 12. September 2009, 12:12 Uhr
Aufgaben des BMT 8 2008 Gruppe A
Druckversion:
Inhaltsverzeichnis |
Aufgabe 1
Aus einem Quader wurde an einer Ecke ein Würfel herausgeschnitten (vergleiche nebenstehende Abbildung). Berechne das Volumen des Restkörpers.
- Das Volumen beträgt 333 cm3.
- möglicher Rechenweg:
- VQuader - VWürfel =
- 5 cm · 12 cm · 6 cm - (12 cm - 9 cm)3 =
- 360 cm3 - 27 cm3 =
- 333 cm3
Aufgabe 2a
Nebenstehende Tabelle zeigt, wie viele Euro-Geldscheine am 31. Mai 2007 in Umlauf waren. Beispielsweise befanden sich von den 200 €-Scheinen 153 Millionen Stück in Umlauf.
Wert Anzahl der Scheine
in Millionen500 € 429 200 € 153 100 € 1116 50 € 3983 20 € 2244 10 € 1804 5 € 1325
Wie hoch war der Gesamtwert aller 50 €-Scheine? (!ca. 200 000 Euro) (!ca. 2 Milliarden Euro) (!ca. 20 Milliarden Euro) (ca. 200 Milliarden Euro) (!ca. 2 Billionen Euro)
Aufgabe 2b
Diese Aufgabe bezieht sich auf die Tabelle aus Aufgabe 2a!
Ungefähr wie viel Prozent aller in Umlauf befindlichen Scheine waren 20 €-Scheine? Die notwendigen Rechnungen brauchen nicht exakt ausgeführt zu werden, es genügt jeweils ein Überschlag. Der Lösungsweg muss nachvollziehbar sein.
- Ungefähr 20 % aller im Umlauf befindlicher Scheine waren 20 € Scheine.
- möglicher Lösungsweg:
- ungefähre Anzahl aller Scheine: 400 + 200 + 1100 + 4000 + 2200 + 1800 + 1300 = 5700 + 4000 + 1300 = 11000
- ungefähre Anzahl der 20 € - Scheine: 2200
= 
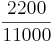= 20 %
Aufgabe 3a
Bestimme die Lösung der Gleichung 12 - 6 · (
x + 3) = 4x.
- x = -1
- möglicher Rechenweg:
- 12 - 6 · (x + 3) = 4x
- 12 - [6 · x + 6 · 3] = 4x Distributivgesetz
- 12 - [2x + 18] = 4x
- 12 - 2x - 18 = 4x Klammer auflösen
- -6 = 6x
- x = -1
- 12 - 6 · (
Aufgabe 3b
Diese Aufgabe bezieht sich auf die Gleichung aus Aufgabe 3a!
Durch welche Zahl muss in obiger Gleichung die Zahl 12 ersetzt werden, damit x = 0 Lösung der neuen Gleichung ist?
- 12 muss durch 18 ersetzt werden.
- möglicher Lösungsweg:
- Mit x = 0 und z für die gesuchte Zahl ergibt sich folgende Gleichung:
- z - 6 · 3 = 0
- Also ist die Zahl 12 durch die Zahl 18 zu ersetzen.
Aufgabe 4a
Im Rahmen des Verkehrsunterrichts wurden die Fahrräder der Unterstufenschüler überprüft. Die einzelnen Mängel wurden in folgender Liste zusammengefasst:
- mangelhafte Beleuchtung an jedem 6. Fahrrad
- mangelhafte Bremsen an 15 % der Fahrräder
- mangelhafte Reifen an der Fahrräder
Welcher Mangel wurde am häufigsten festgestellt? Begründe deine Antwort durch einen Größenvergleich der in der Liste genannten Anteile.
- Am häufigsten wurden mangelhafte Reifen festgestellt.
- mögliche Begründung durch Größenvergleich in der Bruchdarstellung:
- mangelhafte Beleuchtung: "Jedes 6. Fahrrad" entspricht
aller Fahrräder
- mangelhafte Bremsen: 15% =
= 
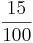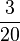
- mangelhafte Reifen:
- mangelhafte Beleuchtung: "Jedes 6. Fahrrad" entspricht
- Größenvergleich der Brüche:
- >
- =
>
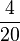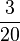
- Der Bruch hat den größten Wert, der zugehörigen Mangel wurde am häufigsten festgestellt.
- mögliche Begründung durch Größenvergleich in der Prozentdarstellung:
- mangelhafte Beleuchtung: entspricht ca. 17%
- mangelhafte Bremsen: 15%
- mangelhafte Reifen: = 20%
- mangelhafte Beleuchtung:
Aufgabe 4b
Diese Aufgabe bezieht sich auf die Liste aus Aufgabe 4a!
Peter schaut sich die obige Liste mit den Ergebnissen der Überprüfung an, rechnet kurz und sagt dann: „Nach dieser Liste sind mehr als 50 % aller untersuchten Fahrräder mangelhaft.“ Begründe, dass Peter nicht unbedingt Recht hat.
- Peter berücksichtigt nicht, dass ein Fahrrad auch zwei oder drei der genannten Mängel aufweisen kann.
Aufgabe 5a
Die Summe der Innenwinkel in einem n-Eck beträgt (n-2)·180°.
Wie viele Ecken hat ein n-Eck mit der Innenwinkelsumme 720°?
- Es hat 6 Ecken.
- Begründung:
- 720° = 4 · 180°
- Also ist n - 2 = 4 und damit n = 6.
Aufgabe 5b
Ein n-Eck mit lauter gleich langen Seiten und gleich großen Innenwinkeln heißt reguläres n-Eck. Berechne die Größe eines Innenwinkels im regulären Zehneck.
- Die Größe des Innenwinkels beträgt 144°.
- möglicher Lösungsweg:
- Zehneck: n = 10
- Innenwinkelsumme (10 - 2)·180° = 1440°
- Größe eines der zehn gleich großen Innenwinkel: 144°
Aufgabe 6a
Von einer Raute sind die Diagonalenlängen e und f bekannt. Überlege, wie man daraus den Flächeninhalt der Raute ermitteln kann, und gib eine entsprechende Formel an.
- A = 0,5 · e · f
- Mögliche Begründung:
- Datei:BMT8 08 A6a 01.jpg Die beiden Diagonalen teilen die Raute in vier gleiche rechtwinkligen Dreiecke. Gruppiert man die Dreiecke um, erhält man ein Rechteck mit z.B. den Kantenlängen 0,5·e und f. Der Flächeninhalt des Rechtecks (und damit der der Raute) beträgt 0,5·e·f.
- weitere Möglichkeiten:
- Datei:BMT8 08 A6a 02.jpgDatei:BMT8 08 A6a 03.jpg
Aufgabe 6b
Konstruiere nur mit Zirkel und Lineal eine Raute, bei der ein Innenwinkel 60° beträgt.
- Zeichne eine beliebige Strecke [AB] der Länge a.
- Zeichne zwei Kreise mit dem Radius a und den Mittelpunkten A und B. Der Schnittpunkt der beiden Kreise ist der Eckpunkt D der Raute.
- Zeichne zwei Kreise mit dem Radius a und den Mittelpunkten B und D. Der Schnittpunkt der beiden Kreise ist der Eckpunkt C der Raute.
Aufgabe 7
Berechne den Wert des Terms 0,1 · (2,4 : 0,6).
- Der Wert des Terms beträgt 0,4.
- Möglicher Rechenweg:
- 0,1 · (2,4 : 0,6) = 0,1 · (24 : 6) = 0,1 · 4 = 0,4
Aufgabe 8a
Gib zwei Zahlen mit verschiedenen Vorzeichen an, so dass auf der Zahlengeraden die Zahl 20 in der Mitte zwischen diesen beiden Zahlen liegt.
- z.B.-10 und 50
- Begründung:
- Datei:BMT8:08 A08a.jpg
- Geht man von der Zahl 20 aus 30 nach links, kommt man zur Zahl -10.
- Geht man von der Zahl 20 aus 30 nach rechts, kommt man zur Zahl 50.
Aufgabe 8b
Bestimme den Mittelwert der Zahlen und 
.
- Der Mittelwert der beiden Zahlen ist
.
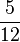- Lösung durch Rechnung:
- ( + ) : 2 =
- (
+ 
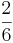) : 2 = Hauptnenner bilden
: 2 =
-
- (
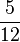
- Überlegung am Zahlenstrahl:
- Datei:BMT8:08 A08b.jpg
- Es gilt: = =
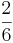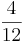und = = 
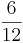
- Der Bruch 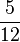liegt genau in der Mitte zwischen 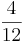und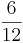
Aufgabe 9a
Die Nationalfahne der Schweiz zeigt ein weißes Kreuz auf rotem Grund. Für die vier kongruenten Arme des Kreuzes ist durch Beschluss der Schweizer Bundes- versammlung aus dem Jahr 1889 festgelegt: Die Länge l eines Arms ist um der Breite b größer als b (vergleiche nebenstehende Abbildung).
Wie lang ist ein Arm, wenn seine Breite 18 cm beträgt?
- Der Arm ist 21 cm lang.
- mögliche Lösungswege:
- l = b + b = 18 cm + 3 cm = 21 cm
- oder
- l = b 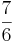+ b =
b = 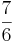·18 cm = (18 cm : 6)· 7 = 21 cm
- l = b +
Aufgabe 9b
Stelle einen Term auf, der den Flächeninhalt des weißen Kreuzes in Abhängigkeit von der Breite b eines Arms beschreibt. Fasse den Term, in dem nur noch b als Variable vorkommen soll, so weit wie möglich zusammen.
- A =
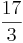b2
- Möglicher Lösungsweg:
- A = 4 · l·b + b2 = 4 · 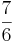b · b + b2 =
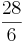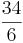b2 + b2 =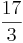 
b2 = b2
- A = 4 · l·b + b2 = 4 ·
