Übungen1: Unterschied zwischen den Versionen
(test) |
|||
| Zeile 5: | Zeile 5: | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | <big>f(x)= 3,5x<sup>2</sup></big> (!Parabel ist nach unten geöffnet) (Parabel ist nach oben geöffnet) (!Parabel ist enger als die Normalparabel) (Parabel ist weiter als die Normalparabel) (Der Punkt | + | <big>f(x)= 3,5x<sup>2</sup></big> (!Parabel ist nach unten geöffnet) (Parabel ist nach oben geöffnet) (!Parabel ist enger als die Normalparabel) (Parabel ist weiter als die Normalparabel) (Der Punkt <math>(2|14)</math> liegt auf dem Graphen) (!Der Punkt [14/2] liegt nicht auf dem Graphen) |
<big>f(x)= -0,5x<sup>2</sup></big> (Parabel ist nach unten geöffnet) (!Parabel ist nach oben geöffnet) (Parabel ist enger als die Normalparabel) (!Parabel ist weiter als die Normalparabel) (Der Punkt [2/-2] liegt auf dem Graphen) (!Der Punkt [2/2] liegt auf dem Graphen) | <big>f(x)= -0,5x<sup>2</sup></big> (Parabel ist nach unten geöffnet) (!Parabel ist nach oben geöffnet) (Parabel ist enger als die Normalparabel) (!Parabel ist weiter als die Normalparabel) (Der Punkt [2/-2] liegt auf dem Graphen) (!Der Punkt [2/2] liegt auf dem Graphen) | ||
Version vom 15. Februar 2009, 17:34 Uhr
Quadratische Funktionen/Übungen - Quadratische Funktionen/Übungen1
Multiple choice
f(x)= 3,5x2 (!Parabel ist nach unten geöffnet) (Parabel ist nach oben geöffnet) (!Parabel ist enger als die Normalparabel) (Parabel ist weiter als die Normalparabel) (Der Punkt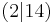 
liegt auf dem Graphen) (!Der Punkt [14/2] liegt nicht auf dem Graphen)
f(x)= -0,5x2 (Parabel ist nach unten geöffnet) (!Parabel ist nach oben geöffnet) (Parabel ist enger als die Normalparabel) (!Parabel ist weiter als die Normalparabel) (Der Punkt [2/-2] liegt auf dem Graphen) (!Der Punkt [2/2] liegt auf dem Graphen)
f(x)= -2x2 (Parabel ist nach unten geöffnet) (!Parabel ist nach oben geöffnet) (!Parabel ist enger als die Normalparabel) (Parabel ist weiter als die Normalparabel) (!Der Punkt [0/-2] liegt auf dem Graphen) (Der Punkt [1/2] liegt oberhalb des Graphen)
Variante 5
Ordne den Funktionsgraphen den richtigen Term zu
 |
 |
|
|
|
|
| 0,5x2 | 2x2 | 3x2 | 0,8x2 | 1,5x2 | 0,75x2 |
